Производные функций, не являющихся явно заданными.
1) Производные функций, заданных параметрически. Если 2) Производная неявной функции. Если а) вычислить производную по х от левой части уравнения, считая y функцией от х; б) приравнять эту производную к нулю; в) решить полученное уравнение относительно 3) Логарифмическая производная используется, если переменная х содержится и в основании, и в показателе степени. 1. Найдите а) 2. Найдите а) 3. Найти производную неявно заданной функции: а) д) 4. Найти логарифмическую производную: а) д)
|

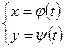 , то
, то 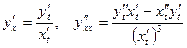 .
.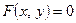 , то:
, то: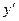 .
. и
и 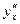 , если
, если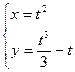 ; б)
; б)  .
.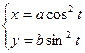 ; б)
; б) 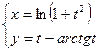 ; в)
; в) 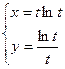 при
при 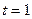 ; г)
; г)  при
при  .
. ; б)
; б)  ; в)
; в)  ; г)
; г) 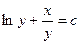 ;
;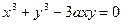 ; е)
; е) 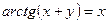 ; ж)
; ж) 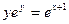 .
. ; б)
; б) 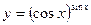 ; в)
; в)  ; г)
; г) 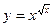 ;
;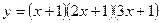 ; е)
; е) 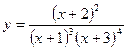 ; ж)
; ж) 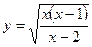 .
.


