Машина Тьюринга

Задание

 

1. На ленте записан текст на английском языке без знаков препинания. Необходимо разработать машину Тьюринга, которая заменяет первое вхождение слова ‘da’ на слово ‘net’. Головка находится в каноническом расположении.

 

2. Доказать частичную рекурсивность функции .

3. На входной ленте записано число S, число N и массив целых чисел длины N. Вычислить и записать на выходную ленту сумму элементов массива, больших S.

 

Машина Тьюринга

 

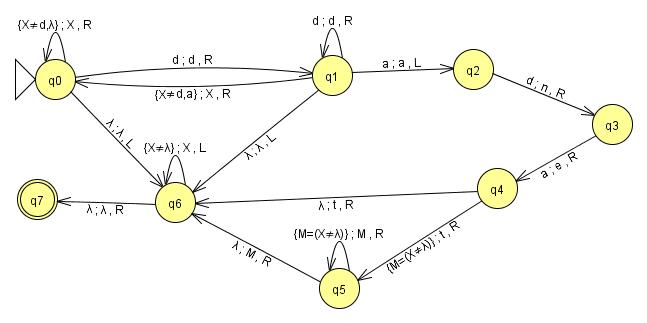
2.1. Теоретические сведения о МТ

Машина Тьюринга – абстрактная вычислительная машина, предложенная Аланом Тьюрингом в 1936 году для формализации понятия алгоритма.

Машина Тьюринга является расширением конечного автомата и, согласно тезису Чёрча — Тьюринга, способна имитировать все другие исполнители (с помощью задания правил перехода), каким-либо образом реализующие процесс пошагового вычисления, в котором каждый шаг вычисления достаточно элементарен. На машине Тюринга также воспроизводим, по сути, любой алгоритм.

Конкретная машина Тьюринга задаётся перечислением элементов множества букв алфавита A, множества состояний Q и набором правил, по которым работает машина. Они имеют вид: q_ia_j→q_i1a_j1d_k (если головка находится в состоянии q_i, а в обозреваемой ячейке записана буква a_j, то головка переходит в состояние q_i1, в ячейку вместо a_jзаписывается a_j1, головка делает движение d_k, которое имеет три варианта: на ячейку влево (L), на ячейку вправо (R), остаться на месте (N)). Для каждой возможной конфигурации <q_i, a_j> имеется ровно одно правило (для недетерминированной машины Тьюринга может быть большее количество правил). Правил нет только для заключительного состояния, попав в которое машина останавливается. Кроме того, необходимо указать конечное и начальное состояния, начальную конфигурацию на ленте и расположение головки машины.

 

2.2. Формализация задачи и описание алгоритма решения

 

Формальная постановка задачи: заменить в подаваемой на ленту строке первое вхождение подстроки “da” на подстроку “net” сдвинув для этого следующую за подстрокой часть строки на один символ вправо.

Решение задачи будет проходить в четыре этапа:

1. Поиск подстроки “da”.
   Если “da” не входит в исходную строку, то алгоритм завершает работу.
   Если найдено первое вхождение “da”, то:
2. Замена “da” на “net”
3. Сдвиг правой части строки вправо на один символ
4. Возврат каретки в начальную позицию

 

 

2.3. Граф переходов МТ

 

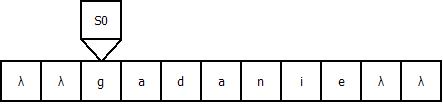
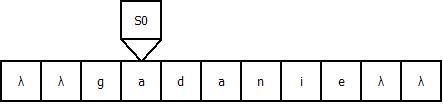
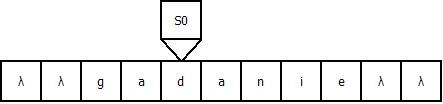
2.4. Вычислительный процесс МТ

 

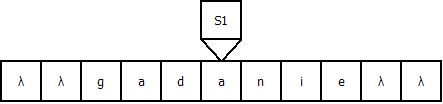
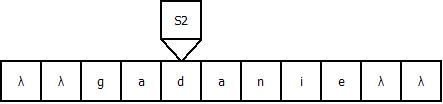
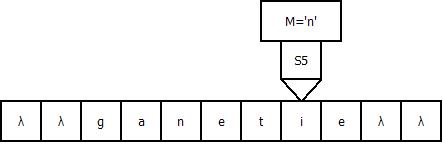
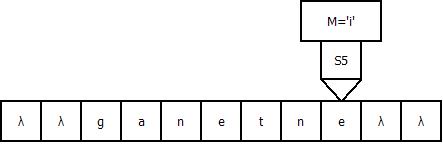
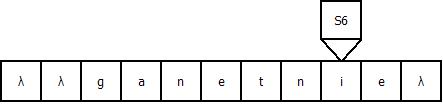
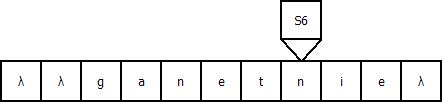
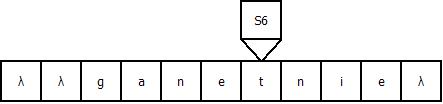
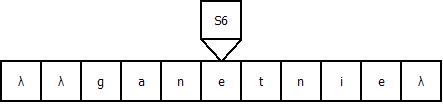
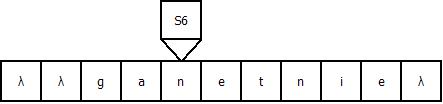
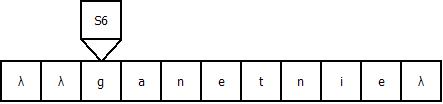
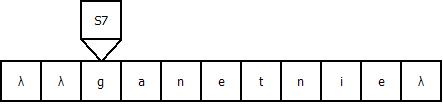
Продемонстрируем работу МТ на примере входной строки “gadanie”: