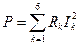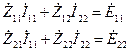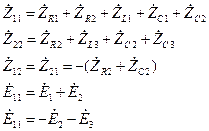Расчет параметров электрических цепей.

Пример 1. Дана электрическая цепь (рис.1) с известными параметрами:

Рис.1

Для расчета в Matlab вводим начальные значения (Iи à Is):

>> R=[10 20 30 40 50 60];

>> E=[10 20 30];

>> Is=[1 2 3];

В методе контурных токов при составлении системы уравнений необходимо заменить источники токов эквивалентными источниками ЭДС. Условием эквивалентности источников являются одинаковые токи и напряжения, вызываемые ими на одной и той же нагрузке (рис.2, 3):

Рис.2

Рис.3

Эквивалентные источники ЭДС (E’ à Es):

>> Es=R(1:3).*Is

 

Es =

 

10 40 90

В методе контурных токов нам необходимо составить систему из 3 (в нашем случае) уравнений:

где - собственное сопротивление контуров.

- общие сопротивления i - го и k- го контуров.

- контурные э. д. с., алгебраическая сумма э. д. с. в каждом контуре.

Следует отметить, что при одинаковом направлении контурных токов в системе уравнений суммы сопротивлений, принадлежащих каждому контуру - собственное сопротивление контуров, входят со знаком плюс, а общие сопротивления двух контуров входят со знаком минус.

Для полученной схемы (рис.3) имеем:

Сформируем и выведем (для контроля) матрицу контурных сопротивлений в Matlab:

>> RR=[R(1)+R(2)+R(5), -R(2), -R(5)

-R(2), R(3)+R(2)+R(4), -R(4)

-R(5), -R(4), R(4)+R(6)+R(5)]

 

RR =

 

80 -20 -50

-20 90 -40

-50 -40 150

и вектор-столбец контурных ЭДС:

>> EE=[E(1)+Es(1)-E(2)-Es(2); E(2)+Es(2)-E(3)-Es(3); 0]

 

EE =

 

-40

-60

Решая контурные уравнения, определим контурные токи:

>> II=RR\EE

 

II =

 

-1.3220

-1.3118

-0.7905

Определив контурные токи, найдем токи в ветвях:

>> I=[II(1); II(2)-II(1); -II(2); II(2)-II(3);...

II(3)-II(1); II(3)]

 

I =

 

-1.3220

0.0102

1.3118

-0.5213

0.5315

-0.7905

При протекании токов через сопротивления в них выделяется мощность

>> P1=sum(R'.*I.^2)

 

P1 =

 

131.5843

Мощность, отдаваемая источниками ЭДС и источниками токов

>> P2=sum(I(1:3)'.*(E+Es))

 

P2 =

 

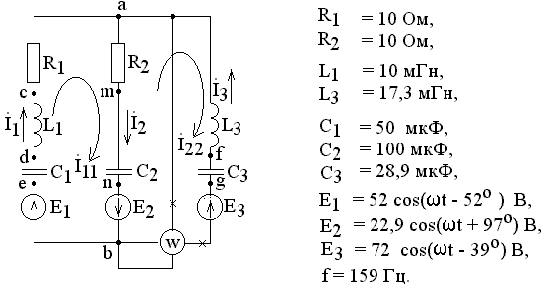
131.5843

Таким образом, баланс мощностей в электрической цепи выполняется.

Пример 2. Дана электрическая цепь (рис.44).

Рис.4

Для расчета в Matlab вводим начальные значения:

>> R=[10, 10, 0];

>> L=[10, 0, 17.3]*1e-3;

>> C=[50, 100, 28.9]*1e-6;

>> E=[52*exp(-j*52*pi/180), 22.9*exp(j*97*pi/180),...

72*exp(-j*39*pi/180)];

 

>> w=2*pi*159;

Введем также комплексные сопротивления для отдельных элементов цепи:

Matlab:

>> ZR=R;

>> ZL=j*w*L;

>> ZC=-j./(w*C1);

Для определения действующих значений токов во всех ветвях будем также использовать метод контурных токов. Для этого запишем систему уравнений:

где соответствующие компоненты определяются как:

Запишем это средствами Matlab:

>> ZZ(1,1)=ZR(1)+ZR(2)+ZL(1)+ZC(1)+ZC(2);

>> ZZ(2,2)=ZR(2)+ZL(3)+ZC(2)+ZC(3);

>> ZZ(1,2)=-(ZR(2)+ZC(2));

>> ZZ(2,1)=ZZ(1,2);

>> EE=[E(1)+E(2); -E(2)-E(3)];

Решая контурные уравнения, определим контурные токи:

>> II=ZZ\EE

 

II =

 

0.7155 - 0.4814i

-0.9408 - 1.5137i

выделяя абсолютное значение и фазу, получим

>> IIE=[abs(II), angle(II)*180/pi]

 

IIE =

 

0.8624 -33.9332

1.7823 -121.8612

Токи в ветвях:

>> I=[II(1); II(1)-II(2); -II(2)];

>> IE=[abs(I), angle(I)*180/pi]

 

IE =

 

0.8624 -33.9332

1.9517 31.9329

1.7823 58.1388

Формируем вектор напряжений:

>> U=I(1)*[ZR(1); ZL(1); ZC(1)]

 

U =

 

7.1555 - 4.8143i

4.8096 + 7.1485i

-9.6380 -14.3249i

Строим Векторную диаграмму (рис. 5):

>> compass(U)

>> hold on

>> compass(I(1)*20,'r')

>> text(real(U(1)),imag(U(1)),'UR1')

>> text(real(U(2)),imag(U(2)),'UL1')

>> text(real(U(3)),imag(U(3)),'UC1')

 

Рис.5