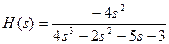Расчет частотных характеристик электрических цепей.
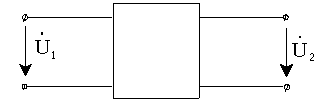
MATLAB и его пакеты расширения ориентированы прежде всего ориентированы на цифровую обработку сигналов, поэтому функции, связанные с расчетом аналоговых цепей, рассматриваются как вспомогательные. В основном они предназначены для вызова из других функций, использующих аналоговые прототипы при синтезе цифровых фильтров. Однако и сами эти функции могут быть весьма полезны. Прежде всего, рассмотрим математическое описание линейных систем, частотные характеристики которых нам необходимо исследовать. Такие линейные системы можно представить в виде четырехполюсника с двумя входными и двумя выходными зажимами (рис.6):
Рис.6 В общем случае, существуют различные эквивалентные способы представления характеристик линейных систем, реализуемых в виде цепей с сосредоточенными параметрами. Но наиболее распространенным является описание с помощью комплексного коэффициента передачи, который представляет собой отношение комплексных выходного
где В не зависимости от параметров электрической цепи, для линейных систем комплексный коэффициент передачи всегда может быть представлен в виде:
где Если мы введем мнимый аргумент
Порядок многочленов в числителе и знаменателе Предположим, что линейная система задается передаточной функцией:
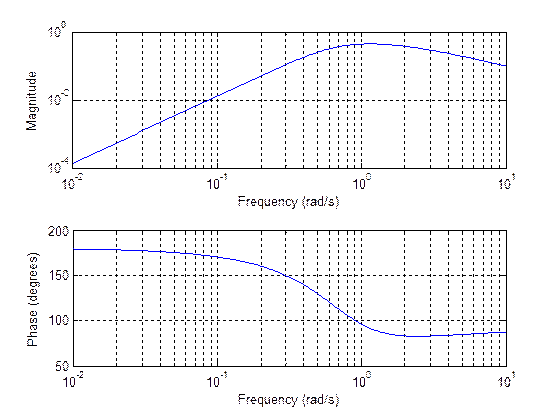
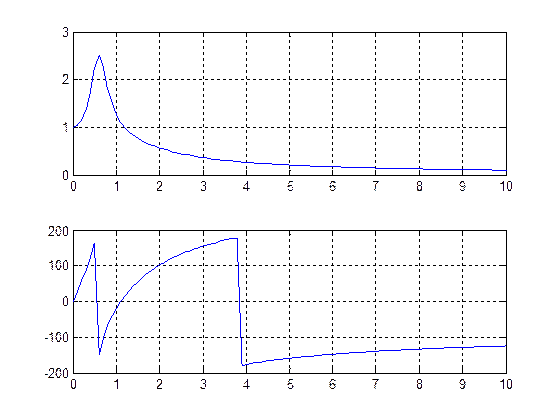
Тогда расчет в MATLAB не взывает труда: w=0:0.1:10; s=j*w; b=[1 3 3 1]; a=[1 -3 4 -2 1]; H=polyval(b,s)./polyval(a,s); subplot(2,1,1); plot(w,abs(H)); grid on; subplot(2,1,2); plot(w,angle(H)*180/pi); grid on; Результатом работы этого скрипта будет графическое окно с графиками, показанными на рис. 7. Верхний – АЧХ, нижний – ФЧХ.
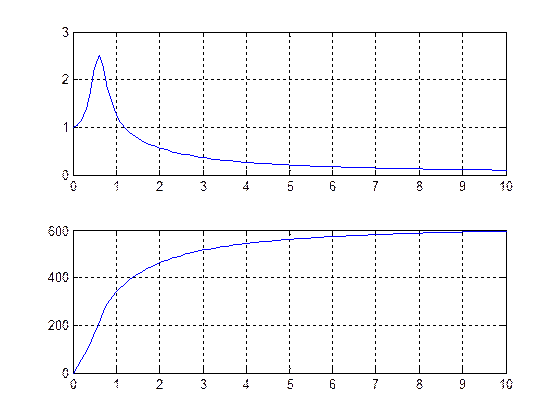
Рис.7 Как видно из рис. 7 ФЧХ имеет разрывы (скачки). Те из них, величина которых равна 180º, действительно являются скачками ФЧХ, а остальные, величина которых составляет 360º, являются «фиктивными». Они возникают из-за того, что результаты вычисления фазы комплексного числа всегда лежа в диапазоне ±180º. Наличие этих многочисленных скачков затрудняет восприятие истинной формы ФЧХ и маскирует скачки «настоящие». Избавиться от лишних разрывов позволяет функция unwrap. Продемонстрируем ее использование: w=0:0.1:10; s=j*w; b=[1 3 3 1]; a=[1 -3 4 -2 1]; H=polyval(b,s)./polyval(a,s); subplot(2,1,1); plot(w,abs(H)); grid on; phi=unwrap(angle(H)); subplot(2,1,2); plot(w,phi*180/pi); grid on;
Рис.8
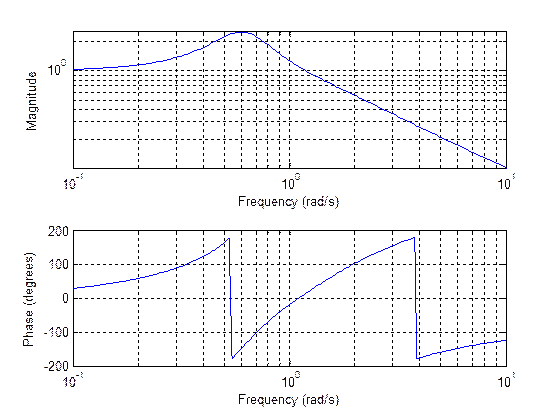
Вычисление и построение АЧХ и ФЧХ, можно также осуществить с помощью функции freqs. В простейшем идее она имеет следующий синтаксис: freqs(b,a) Здесь b и a – векторы коэффициентов полиномов, соответственно числителя и знаменателя функции передачи. Для расчета характеристики по умолчанию выбираются 200 частот, логарифмически равномерно распределенных в диапазоне от 0,1 до 10. При отсутствии выходных параметров функция freqs строит графики АЧХ и ФЧХ. АЧХ – выводится в логарифмическом масштабе (но без пересчета в децибелы), ФЧХ - градусах. Построим АЧХ и ФЧХ из прошлого примера с помощью функция freqs: b=[1 3 3 1]; a=[1 -3 4 -2 1]; freqs(b,a);
Рис.9 Чтобы вместо построения графика получить вектор рассчитанных значений комплексного коэффициента передачи, нужно присвоить результат, возвращаемый функцией freqs. В простейшем идее она имеет следующий синтаксис: H=freqs(b,a); Если использовать второй выходной параметр, то в нем функция возвратит вектор частот, для которых рассчитаны значения характеристики: [H,w]=freqs(b,a); Также можно принудительно задать частоты для анализа – с помощью третьего входного параметра: H=freqs(b,a,w); Приведем пример использования функции freq результатом которого будет графики, представленные на рис. 8: w=0:0.1:10; b=[1 3 3 1]; a=[1 -3 4 -2 1]; H=freqs(b,a,w); subplot(2,1,1); plot(w,abs(H)); grid on; phi=unwrap(angle(H)); subplot(2,1,2); plot(w,phi*180/pi); grid on;
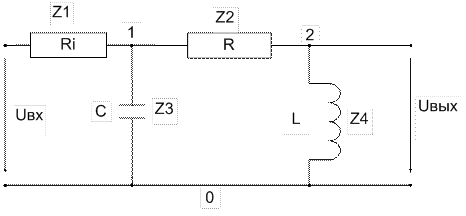
Приведем пример расчета реальной цепи, представленной на рис. 10
Рис.10
Комплексные сопротивления для представленной схемы:
Для определения передаточной функции воспользуемся методом узловых потенциалов. Для этого запишем систему узловых уравнений:
где соответствующие компоненты определяются как:
Здесь
Запишем систем узловых напряжений в виде:
или
Вводя коэффициенты передачи
Выражая из системы интересующий нас коэффициент передачи, получим:
Итак, имеем для значений
Решение всей задачи в MATLAB: syms R1 R2 C1 L1 s Z=[R1, R2, 1/(s*C1), s*L1]; Y=1./Z; YY=[Y(1)+Y(2)+Y(3), -Y(3); -Y(3), Y(2)+Y(4)]; iu=[Y(1); 0]; KK=YY\iu; R1=1;R2=2;C1=1;L1=2; KK=subs(KK); [n d]=numden(KK(2)); b=sym2poly(n); a=sym2poly(d); freqs(b,a);
Рис.11
|

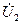 и входного
и входного 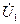 напряжений:
напряжений: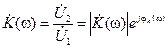
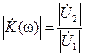 - передаточная АЧХ;
- передаточная АЧХ; 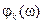 - передаточная ФЧХ.
- передаточная ФЧХ.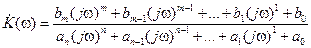
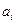 ,
, 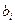 – некоторые постоянные коэффициенты, определяемые параметрами цепи. Необходимо также отметить, что максимальный порядок многочлена числителя не может превышать максимального порядка многочлена стоящего в знаменателе, т.е.
– некоторые постоянные коэффициенты, определяемые параметрами цепи. Необходимо также отметить, что максимальный порядок многочлена числителя не может превышать максимального порядка многочлена стоящего в знаменателе, т.е. 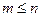 .
.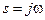 и подставим в выражение для комплексного коэффициента передачи, то получим выражение для передаточной функции линейной системы:
и подставим в выражение для комплексного коэффициента передачи, то получим выражение для передаточной функции линейной системы: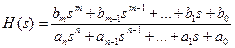
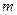 и
и 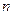 , а также постоянные коэффициенты
, а также постоянные коэффициенты 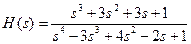
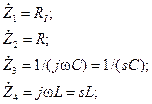
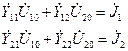
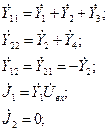
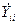 - собственная комплексная проводимость i -узла;
- собственная комплексная проводимость i -узла;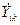 - общая комплексная проводимость между i -м и k -м узлами;
- общая комплексная проводимость между i -м и k -м узлами;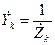 - комплексная проводимость ветвей цепи;
- комплексная проводимость ветвей цепи;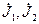 - токи, связанные с узлами
- токи, связанные с узлами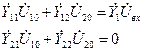
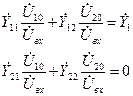
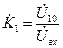 и
и 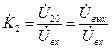 получим:
получим: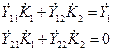
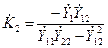
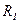 =1Ом;
=1Ом; 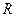 =2Ом;
=2Ом; 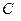 =1Ф;
=1Ф; 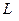 =1Гн
=1Гн