Решение расчетной задачи
Расчетная задача 1. Рассчитать значения и построить график функции ω(t) – параметр потока замен машин при случайном списании по достижении машиной предельного состояния и мгновенной замене ее на новую. Расчет функции ω(t) выполнить для значения t = 1,2,3...,ti, где для ti выполняется условие /ω)(ti) - ω(ti-1)/<0,01 и / ω(ti) - ωП, (1) где ωП — предельное значение функции ω(t) при увеличении времени t. В расчетах использовать предположение о нормальном распределении срока службы машин с заданными значениями параметров μ (математическое ожидание) и σ (среднеквадратичное отклонение). Значение параметров μ = 3,9; σ = 0,9. 2. Для парка, в котором имеется N машин а) рассчитать точное значение математического ожидания, т.е. среднего числа машин, необходимых для замены за 6,5 лет работы от начала существования парка машин; б) определить приближенное значение математического ожидания числа машин, необходимых для замены за период времени работы парка от а1 =7 до b1 = 12, используя линейную аппроксимацию функции ω(t) по рассчитанным значениям; в) определить приближенное значение математического ожидания числа машин, необходимых для замены в установившемся режиме работы парка за период времени от а2=20 до b2=30 и оценить максимальную погрешностьэтого значения. Значения числа машин в парке N= 38 единиц. Решение расчетной задачи 2.Расчет значений функции параметр потока замен Для расчета значений функции параметр потока замен ω(t) используем следующие формулы: (2) где ωП – предельное значение функции ω(t).
где
ωП=0,256; с=0,443 Результаты представлены в таблице 1. Таблица 1
На рисунке 1 представлен график функции ω(t). Точками показаны рассчитанные значения функции от 1 до 13 с шагом h 1. 3. Расчет среднего числа машин, необходимых для замены в парке за заданное время. Проведем расчет среднего числа машин, необходимых для замены в парке из N машин за время t=6,5 лет. Для этого используем следующие формулы:
где
где H(t) –среднее число замен всего парка. Резултаты расчета представлены в таблице 2.
Ω(t)=∑Ф(zi)=1,158
При N=38 за это время в парке потребуется в среднем машин для замены Н(0,6,5)=38*1,158=44 единицы.
4. Расчет приближенного среднего значения числа замен машин в парке с использованием линейной аппроксимации параметра потока замен. Рассчитаем приближенное значение математического ожидания числа замен машин в парке. Численное интегрирование функции проведем с помощью формулы:
Ω(7,12)= 1 {0,5 [w(7)+w(12)]+w(8)+w(9)+w(10)+w(11)}= =0,5(0,261+0,282) + +0,325 +0,258+0,213+0,253=1,321 При числе машин в парке N=38 для замен потребуется в среднем машин: Н(7,12)=38х 1,321=50 единиц 5. Вычисление среднего числа замен машин в парке при больших значениях времени. Вычислим приближенное значение математического ожидания числа замен машин в парке при больших значениях времени t в установившемся режиме, когда можно считать значение функции ω(t) постоянным и равным ωп. При заданных нижней границе интервала а2=20 и верхней границе b2 = 30 погрешности при замене значений функции ω(t) и установившемся значением ωп будут меньше 0,01 Среднее число замен получим по формуле:
Ω(20,30)=0,256х(30-20)=2,56 Среднее число замен машин в парке Н(6,13)=38x2,56=97 единиц
|

 (3)
(3)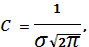 (4)
(4) (5)
(5)
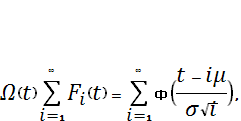 (6)
(6) (7) H(t) = NΩ(t),
(7) H(t) = NΩ(t), Таблица 2
Таблица 2
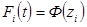
 (8)
(8) (9)
(9)


