Теоретические предпосылки
Я.Ш. Вахитов Физические основы акустики Специальность ЗВУКОРЕЖИССУРА Раздел: «Сложные периодические колебания и их спектры»
Учебное пособие по теории раздела и методике выполнения контрольной работы.
Санкт-Петербург Теоретические предпосылки Звуковые колебания в процессе звукопередачи или записи подвергаются обработке с помощью технических средств звукорежиссуры. Целью этой процедуры является частичное изменение или корректировка субъективных параметров составляющих звукового ряда – их тембров, громкостей, доминантных факторов и т.п. С объективной, т.е. физической, точки зрения звук есть колебания частиц среды, вызываемые распространяющейся в этой среде звуковой волной. С субъективной же или психофизической – это слуховой образ, несущий определенную информацию: семантического (речь), эстетического (музыка) или комплексного (вокальная речь) характера. Между объективными параметрами звуковых колебаний и их субъективным отражением в сознании существует определенная взаимосвязь или корреляция. Основные физические факторы, отвечающие за создание того или иного субъективного эффекта, называются физическими коррелятами (ФК) этого субъективного параметра. Например, ФК высоты звука [1], [2] является частота f1 основного тона периодического музыкального звука, ФК громкости – энергия звука, выражаемая его интенсивностью I или звуковым давлением p. И высота, и громкость звука являются его количественными субъективными параметрами. Существует и качественная субъективная характеристика звуков – это их тембр [3], определяемый в музыке, как окраска звуков. В акустике этому важнейшему параметру придается более широкий смысл: тембром называется субъективная качественная характеристика звука, определяющая его индивидуальную особенность, т.е. его распознаваемость в присутствии любых других звуков. Образно говоря, тембр это визитная карточка конкретного звука. Изучение физических коррелятов тембра выявило важную особенность взаимосвязи физических параметров звуковых колебаний с их субъективными: одни и те же психофизические характеристики звука могут быть обусловлены разными, иногда несколькими, физическими факторами. Так тембр звуков, создаваемых инструментами достаточно длительного (квазистационарного) звучания, зависит от колебательной формы этих звуков, определяющейся их спектрами [3], [4]. К таким инструментам относятся, например, струнные смычковые инструменты (при смычковом возбуждений струны), деревянные и медные духовые и некоторые другие. Тембр звуков, получаемых от инструментов с кратковременным возбуждением (щипком, ударом молоточков и т.п.), зависит не только от формы самого колебания, но в большой мере - от огибающей колебательного процесса вовремени, определяющей длительности и формы атаки, стояния и затухания возбужденного колебания (рис. 1). Однако и в этом случае важную роль в формировании тембральной характеристики звука выполняет спектр колебания. Французский математик Фурье доказал теорему, согласно которой периодическое колебание любой формы – пилообразной, прямоугольной, импульсной (рис. 2) – и других, в том числе не поддающихся аналитическому описанию, можно представить в виде суммы синусоидальных (гармонических) колебаний
называемых гармониками рассматриваемого колебания сложной формы. Каждая К -я гармоника (первая, вторая, третья и т.д.) характеризуется своей амплитудой Yk, частотой fk и начальной фазой φк. Частота первой гармоники (К =1) определяется периодом Т1 рассматриваемого сложного колебания, т.е.
В музыке ее называют частотой основного тона звука, обусловленного данным сложным колебанием. Частоты остальных гармоник выше частоты основного тона и отличаются от нее в целое число раз, совпадающее с номером соответствующей гармоники, т.е. являются целыми кратными частоты основного тона:
Частоты основной гармоники f1 и высших fk, записываемые с помощью символа f, называют циклическими частотами, что соответствует их физическому смыслу: число циклов полных колебаний, совершаемых в одну секунду. Поскольку аргументами функций синус и косинус могут быть только угловые величины, то синусоиды ряда (1) принято представлять в форме
называются угловой (или круговой) частотой соответствующей гармоники. Распределение значений амплитуд Yk и начальных фаз φк зависит от колебательной формы рассматриваемой кривой, т.е. у колебаний различной формы, но одинаковых периодов Т1 и пиковых значений Y0, распределения значений Yk и φк также будут разными. Можно это же выразить по-другому: соотношение величин амплитуд Yk и начальных фаз φк гармоник ряда (1) при их суммировании (по мгновенным значениям) определит форму базового колебания (см. рис. 2). Разложение сложного колебания на составляющие его гармоники (т.е. определение их амплитуд и начальных фаз) называется анализом, а составление его путем сложения гармоник – синтезом этого колебания. Совокупности амплитуд Yк и начальных фаз φк, выстроенные в графической или табличной форме в соответствии с частотам fk этих гармоник, называются соответственно амплитудным и фазовым спектрами базового колебания (см. рис. 2). Помимо этих спектров на практике (например, в микшерных пультах) приходится иметь дело с энергетическими спектрами [3], [4]. В музыкальной, речевой и электроакустике, рассматривая спектры конкретных звуков, обычно имеют в виду амплитудный спектр и не проявляют интереса к фазовому. Дело в том, что слуховое ощущение тембра звука формируется именно амплитудным спектром и не зависит от фазового. Поэтому будущим звукорежиссерам (да и не только им) полезно усвоить некоторые параметры амплитудных спектров периодических звуков (в дальнейшем, говоря «спектр», будем иметь в виду именно амплитудную его часть). К таким параметрам относятся: - спектральный шаг - структура спектра: а) количество гармоник в звуке того или иного музыкального инструмента; б) отсутствие гармоник определенных номеров (четных или нечетных, кратных по номеру некоторым малым числам, например, 3, 4, 5 и т.п.); - огибающая спектра – линия (на рис. 2 – прерывистая), показывающая: а) тенденцию и характер изменения амплитуд (или энергии) спектральных составляющих с частотой; б) наличие или отсутствие формант (абсолютных или относительных). В музыкальной литературе вместо термина «гармоники» часто пользуются термином «обертоны». Следует иметь в виду, во-первых, что нумерация обертонов не сопрягается с нумерацией гармоник. Например, если при используемом способе возбуждения колебаний музыкального инструмента реализуются все гармоники, то первым обертоном будет вторая гармоника, вторым – третья и т.д.. Если же реализуются только те обертоны, которые соответствуют, к примеру, 3, 5, 7 (т.е. нечетным) гармоникам, то первым обертоном будет 3-я гармоника, вторым – 5-я, третьим – 7-я и т.д. (см. рис. 2, б). И, во-вторых, что всякая гармоника является обертоном, но не всякий обертон – гармоникой (т.к. у реальных звуков частоты обертонов могут быть не целыми кратными частоте основного тона f1).
|

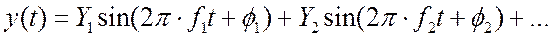 (1)
(1)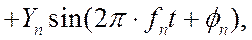
 . (2)
. (2)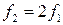 ;
; 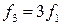 ;
;  . (3)
. (3) , где
, где (4)
(4) , определяющий плотность спектра; он равен частоте основного тона или первой гармоники, т.е.
, определяющий плотность спектра; он равен частоте основного тона или первой гармоники, т.е. 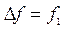 ; плотность спектра является обратной величиной
; плотность спектра является обратной величиной 


