Вихревое электрическое поле. Первое уравнение Максвелла
При изучении электромагнитной индукции мы выяснили, что всякое изменение магнитного поля сопровождается возникновением в замкнутом проводнике индукционного тока за счет появления вихревого электрического поля. Анализируя это явление, Максвелл пришел к выводу, что вихревое электрическое поле появляется всякий раз, когда изменяется магнитное поле, независимо от того, имеются ли в данной области пространства проводники. Последние играют вспомогательную роль и являются всего лишь индикаторами возникновения вихревого электрического поля. Запишем данный результат в математической форме. Для этого в формуле закона электромагнитной индукции (4.1) представим ЭДС как циркуляцию вектора напряженности электрического поля (2.5), а элементарный магнитный поток - в виде (3.16). Получим:
Полученное уравнение называется первым уравнением Максвелла в интегральной форме. Проиллюстрируем это уравнение рисунком 10.1. Пусть в некоторой области пространства магнитная индукция направлена вверх и возрастает по величине: Знак магнитного потока через площадку S, ограниченную контуром L, зависит от направления нормали правилом буравчика (см. раздел 3.3). В случае, показанном на рис. 10.1, нормаль совпадает по направлению с вектором магнитной индукции
|
. Поскольку операции дифференцирования и интегрирования в правой части уравнения проводятся по разным переменным, их можно поменять местами: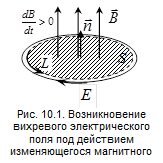
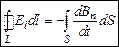. (10.1)
.
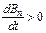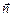к площадке. Положительное направление нормали связано с направлением обхода контура
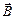, поэтому подынтегральное выражение в правой части формулы (10.1) будет положительным, а циркуляция вектора напряженности электрического поля - отрицательной. Это означает, что во всех точках контура L электрическое поле Е направлено противоположно направлению обхода. Отметим, что линии напряженности электрического поля расположены в плоскости, перпендикулярной вектору магнитной индукции. Аналогичным образом можно вычислить циркуляцию вдоль любого контура.
