Эрстед обнаружил, что электрический ток создает магнитное поле; математически этот факт выражается теоремой о циркуляции магнитной индукции (3.13), которую для поля в магнетике можно записать в виде:
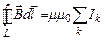 . С учетом (5.21) можно записать теорему о циркуляции напряженности магнитного поля:
. С учетом (5.21) можно записать теорему о циркуляции напряженности магнитного поля:  . (10.2)
. (10.2)
Согласно гипотезе Максвелла, существует и другая причина возникновения магнитного поля. Коль скоро в соответствии с законом электромагнитной индукции Фарадея (гл. 4) изменение магнитного поля приводит к появлению электрического поля, то должно быть справедливо и обратное: изменение электрического поля должно сопровождаться возникновением магнитного поля.
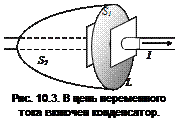
Покажем справедливость гипотезы Максвелла. Применяя теорему о циркуляции вектора магнитной индукции, мы считали, что ток пронизывает плоскую поверхность (S1 на рис. 10.2), ограниченную замкнутым контуром L. Но с таким же успехом можно было бы рассматривать поверхность S2, опирающуюся на тот же контур интегрирования, поскольку эту поверхность пронизывает такой же ток I. Иначе говоря, любую поверхность, опирающуюся на контур интегрирования, пронизывает один и тот же ток. Значит, сила тока, входящего в объем, ограниченный поверхностями S1 и S2, равна силе тока, выходящего из этого объема. Это утверждение, по существу, эквивалентно первому правилу Кирхгофа.
 Применим теперь теорему о циркуляции вектора
Применим теперь теорему о циркуляции вектора 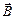 к цепи, в которой происходит разряд конденсатора (рис. 10.3). Поместим поверхность S1 между обкладками конденсатора. Кажется, что для поверхностей S1 и S2 циркуляция будет различной, так как через поверхность S1 ток не протекает (I = 0). Однако эти две поверхности опираются на один и тот же контур, по которому и вычисляется циркуляция, которая должна быть одинаковой в обоих случаях. Максвелл разрешил проблему, связанную с отсутствием тока через поверхность S1, предположив, что изменяющееся электрическое поле между обкладками конденсатора эквивалентноэлектрическому току, который он назвал током смещения. Ток смещения iсм как бы замыкает ток проводимости i, существующий в подводящих проводниках. Исходя из равенства тока смещения через поверхность S1 току проводимости через S2, выразим силу тока смещения через напряженность изменяющегося электрического поля между обкладками конденсатора.
к цепи, в которой происходит разряд конденсатора (рис. 10.3). Поместим поверхность S1 между обкладками конденсатора. Кажется, что для поверхностей S1 и S2 циркуляция будет различной, так как через поверхность S1 ток не протекает (I = 0). Однако эти две поверхности опираются на один и тот же контур, по которому и вычисляется циркуляция, которая должна быть одинаковой в обоих случаях. Максвелл разрешил проблему, связанную с отсутствием тока через поверхность S1, предположив, что изменяющееся электрическое поле между обкладками конденсатора эквивалентноэлектрическому току, который он назвал током смещения. Ток смещения iсм как бы замыкает ток проводимости i, существующий в подводящих проводниках. Исходя из равенства тока смещения через поверхность S1 току проводимости через S2, выразим силу тока смещения через напряженность изменяющегося электрического поля между обкладками конденсатора.
Изменение заряда конденсатора q вызывается током в проводниках, поэтому: 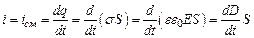 , где s - поверхностная плотность заряда на пластинах конденсатора, S – площадь пластин конденсатора,
, где s - поверхностная плотность заряда на пластинах конденсатора, S – площадь пластин конденсатора,  – электрическое смещение. При выводе была использована формула для напряженности поля в конденсаторе E=s/ee0. Плотность тока смещения будет равна
– электрическое смещение. При выводе была использована формула для напряженности поля в конденсаторе E=s/ee0. Плотность тока смещения будет равна 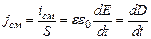 .
.
Справедливо также векторное соотношение:
 (10.3)
(10.3)
Плотность тока смещения[1] равна производной от электрического смещения по времени.
В рассмотренном выше случае токи проводимости и смещения были разделены в пространстве, поэтому теорему о циркуляции (10.2) можно представить в виде: 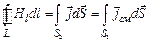 . Сумму токов, охватываемых контуром, мы заменили интегралом по поверхности S1, сквозь которую протекает ток смещения, либо равным ему интегралом по поверхности S2, сквозь которую протекает ток проводимости.
. Сумму токов, охватываемых контуром, мы заменили интегралом по поверхности S1, сквозь которую протекает ток смещения, либо равным ему интегралом по поверхности S2, сквозь которую протекает ток проводимости.
В общем случае внутри контура интегрирования могут быть как токи проводимости, так и токи смещения, поэтому теорема о циркуляции будет выглядеть следующим образом:
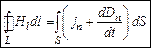 . (10.4)
. (10.4)
в котором скалярное произведение 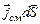 представлено в виде:
представлено в виде:
 ,
,
Аналогично представлено скалярное произведение 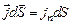 .
.
Уравнение (10.4) называют вторым уравнением Максвелла в интегральной форме. Оно выражает идею Максвелла о том, что магнитное поле создается токами проводимости и переменным электрическим полем.
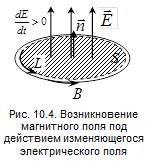 Проиллюстрируем второе уравнение Максвелла. Пусть в некоторой области пространства, заполненной веществом, электрические и магнитные свойства которого одинаковы во всех точках, вектор электрического смещения направлен вверх и возрастает по величине:
Проиллюстрируем второе уравнение Максвелла. Пусть в некоторой области пространства, заполненной веществом, электрические и магнитные свойства которого одинаковы во всех точках, вектор электрического смещения направлен вверх и возрастает по величине:  (рис.10.4). Если в этой области отсутствуют токи проводимости, уравнение (10.4) будет иметь вид:
(рис.10.4). Если в этой области отсутствуют токи проводимости, уравнение (10.4) будет иметь вид:  или
или
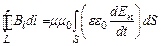 . Поскольку ин интегрирование и дифференцирование в правой части последнего выражения проводятся по разным переменным, эти операции можно поменять местами:
. Поскольку ин интегрирование и дифференцирование в правой части последнего выражения проводятся по разным переменным, эти операции можно поменять местами:
 .
.
Интеграл 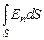 есть не что иное, как поток вектора напряженности электрического поля. Знак потока через площадку S, ограниченную контуром L, зависит от направления нормали
есть не что иное, как поток вектора напряженности электрического поля. Знак потока через площадку S, ограниченную контуром L, зависит от направления нормали 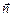 к площадке, а направление последней связано с направлением обхода контура правилом буравчика. В случае, показанном на рис. 10.4, знак потока будет положительным, производная от потока также положительна (поле возрастает), и знак циркуляции вектора магнитной индукции поля положителен. Это означает, что во всех точках контура L линия индукции магнитного поля В направлена по направлению обхода. Отметим, что линии магнитной индукции расположены в плоскости, перпендикулярной вектору напряженности электрического поля.
к площадке, а направление последней связано с направлением обхода контура правилом буравчика. В случае, показанном на рис. 10.4, знак потока будет положительным, производная от потока также положительна (поле возрастает), и знак циркуляции вектора магнитной индукции поля положителен. Это означает, что во всех точках контура L линия индукции магнитного поля В направлена по направлению обхода. Отметим, что линии магнитной индукции расположены в плоскости, перпендикулярной вектору напряженности электрического поля.

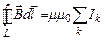 . С учетом (5.21) можно записать теорему о циркуляции напряженности магнитного поля:
. С учетом (5.21) можно записать теорему о циркуляции напряженности магнитного поля:  . (10.2)
. (10.2)
 Применим теперь теорему о циркуляции вектора
Применим теперь теорему о циркуляции вектора 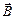 к цепи, в которой происходит разряд конденсатора (рис. 10.3). Поместим поверхность S1 между обкладками конденсатора. Кажется, что для поверхностей S1 и S2 циркуляция будет различной, так как через поверхность S1 ток не протекает (I = 0). Однако эти две поверхности опираются на один и тот же контур, по которому и вычисляется циркуляция, которая должна быть одинаковой в обоих случаях. Максвелл разрешил проблему, связанную с отсутствием тока через поверхность S1, предположив, что изменяющееся электрическое поле между обкладками конденсатора эквивалентноэлектрическому току, который он назвал током смещения. Ток смещения iсм как бы замыкает ток проводимости i, существующий в подводящих проводниках. Исходя из равенства тока смещения через поверхность S1 току проводимости через S2, выразим силу тока смещения через напряженность изменяющегося электрического поля между обкладками конденсатора.
к цепи, в которой происходит разряд конденсатора (рис. 10.3). Поместим поверхность S1 между обкладками конденсатора. Кажется, что для поверхностей S1 и S2 циркуляция будет различной, так как через поверхность S1 ток не протекает (I = 0). Однако эти две поверхности опираются на один и тот же контур, по которому и вычисляется циркуляция, которая должна быть одинаковой в обоих случаях. Максвелл разрешил проблему, связанную с отсутствием тока через поверхность S1, предположив, что изменяющееся электрическое поле между обкладками конденсатора эквивалентноэлектрическому току, который он назвал током смещения. Ток смещения iсм как бы замыкает ток проводимости i, существующий в подводящих проводниках. Исходя из равенства тока смещения через поверхность S1 току проводимости через S2, выразим силу тока смещения через напряженность изменяющегося электрического поля между обкладками конденсатора.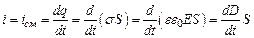 , где s - поверхностная плотность заряда на пластинах конденсатора, S – площадь пластин конденсатора,
, где s - поверхностная плотность заряда на пластинах конденсатора, S – площадь пластин конденсатора,  – электрическое смещение. При выводе была использована формула для напряженности поля в конденсаторе E=s/ee0. Плотность тока смещения будет равна
– электрическое смещение. При выводе была использована формула для напряженности поля в конденсаторе E=s/ee0. Плотность тока смещения будет равна 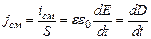 .
. (10.3)
(10.3)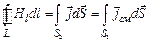 . Сумму токов, охватываемых контуром, мы заменили интегралом по поверхности S1, сквозь которую протекает ток смещения, либо равным ему интегралом по поверхности S2, сквозь которую протекает ток проводимости.
. Сумму токов, охватываемых контуром, мы заменили интегралом по поверхности S1, сквозь которую протекает ток смещения, либо равным ему интегралом по поверхности S2, сквозь которую протекает ток проводимости.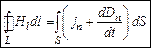 . (10.4)
. (10.4)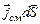 представлено в виде:
представлено в виде: ,
,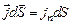 .
. Проиллюстрируем второе уравнение Максвелла. Пусть в некоторой области пространства, заполненной веществом, электрические и магнитные свойства которого одинаковы во всех точках, вектор электрического смещения направлен вверх и возрастает по величине:
Проиллюстрируем второе уравнение Максвелла. Пусть в некоторой области пространства, заполненной веществом, электрические и магнитные свойства которого одинаковы во всех точках, вектор электрического смещения направлен вверх и возрастает по величине:  (рис.10.4). Если в этой области отсутствуют токи проводимости, уравнение (10.4) будет иметь вид:
(рис.10.4). Если в этой области отсутствуют токи проводимости, уравнение (10.4) будет иметь вид:  или
или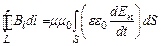 . Поскольку ин интегрирование и дифференцирование в правой части последнего выражения проводятся по разным переменным, эти операции можно поменять местами:
. Поскольку ин интегрирование и дифференцирование в правой части последнего выражения проводятся по разным переменным, эти операции можно поменять местами: .
.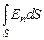 есть не что иное, как поток вектора напряженности электрического поля. Знак потока через площадку S, ограниченную контуром L, зависит от направления нормали
есть не что иное, как поток вектора напряженности электрического поля. Знак потока через площадку S, ограниченную контуром L, зависит от направления нормали 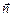 к площадке, а направление последней связано с направлением обхода контура правилом буравчика. В случае, показанном на рис. 10.4, знак потока будет положительным, производная от потока также положительна (поле возрастает), и знак циркуляции вектора магнитной индукции поля положителен. Это означает, что во всех точках контура L линия индукции магнитного поля В направлена по направлению обхода. Отметим, что линии магнитной индукции расположены в плоскости, перпендикулярной вектору напряженности электрического поля.
к площадке, а направление последней связано с направлением обхода контура правилом буравчика. В случае, показанном на рис. 10.4, знак потока будет положительным, производная от потока также положительна (поле возрастает), и знак циркуляции вектора магнитной индукции поля положителен. Это означает, что во всех точках контура L линия индукции магнитного поля В направлена по направлению обхода. Отметим, что линии магнитной индукции расположены в плоскости, перпендикулярной вектору напряженности электрического поля.


