Теорія стійкості дисперсних систем Дєрягіна, Ландау Фервея і Овербека
Розглянемо коагуляцію дисперсної системи під дією електролітів. Найменша концентрація електроліту, при якій начинається коагуляція називається порогом коагуляції (Сп). Концентрація електроліту, при якій коагуляція стає швидкою і подальше збільшення концентрації не впливає на швидкість коагуляції, називається критичною концентрацією або порогом швидкої коагуляції (Скр) рис.55.
Рис. 55. Залежність швидкості коагуляції від концентрації електроліту.
Коагуляцію викликає іон, знак заряду якого протилежний до знаку заряду колоїдної частинки. Сучасна фізична теорія стійкості колоїдних систем була запропонована Б.В. Дєрягіним і Л.Д.Ландау в 1937 - 1941 роках, а пізніше незалежно від них Фервеєм і Овербеком і названа за першими літерами їх прізвищ – теорія ДЛФО. В теорії враховується тільки електростатичний фактор стійкості. Теорія розглядає процес коагуляції як результат спільної дії сил молекулярного притягання та електростатичного відштовхування між частинками. В залежності від балансу цих сил в тонкому прошарку між частинками при їх наближенні виникає позитивний розклинювальний тиск, який перешкоджає їх злипанню, або негативний, що призводить до злипання частинок. Теорія розглядає настільки великі частинки, що можна нехтувати їх тепловим рухом. Лінійний розмір частинок значно більший за товщину подвійного електричного шару, тоді їх взаємодію можна розглядати, як взаємодію двох плоских пластин. Енергію відштовхування приймають за додатню, а притягання - від’ємну. Сумарну енергію системи із двох частинок одержують додаванням енергії відштовхування і енергії притягання: US = Ue + Uм (7.6) US - сумарна енергія взаємодії; Ue - енергія електростатичного відштовхування; Uм – енергія молекулярного притягання.
Рис. 56. Схема взаємодії між двома частинками.
Сили відштовхування, згідно з теорією ДЛФО, мають електростатичну природу. Їх треба розглядати не як кулонівську взаємодію заряджених частинок, а як взаємодію дифузійних шарів міцел. Вони проявляються, тоді коли дві однаково заряджені частинки наближаються настільки, що їх дифузні шари перекриваються. Енергія відштовхування зменшується з відстанню за експонентою. Для малих значень потенціалу поверхні (j<25 мВ) енергія відштовхування частинок дорівнює:
h – відстань між частинками. Для великих значень потенціалу поверхні:
cо – концентрація іонів в розчині; g – коефіцієнт, що залежить від потенціалу поверхні, та заряду іонів. Енергія молекулярного притягання між частинками змінюється обернено пропорційно квадрату відстані між частинками і дорівнює:
А – стала Гамакера, яка враховує природу частинок і шарів, що їх оточують. Складові енергії взаємодії між частинками мають різні знаки, тому знак сумарної енергії залежить від того, яка з них переважає. Аналіз потенційної кривої сумарної енергії взаємодії дає змогу виділити на ній такі характерні ділянки (Рис.51,а): 1)В області малих відстаней (2-10 нм) на кривій є глибокий первинний мінімум (потенціальна яма), який вказує на значну перевагу енергії притягання. Глибина первинної потенціальної ями може досягати (20 - 25) kT. 2)В області середніх відстаней (10-100 нм) на кривій є максимум, який утворює енергетичний бар’єр сил відштовхування, величина якого зумовлює агрегативну стійкість системи. Висота бар’єра змінюється від 0 до 100 kT в залежності від концентрації електролітів в системі. 3)В області великих відстаней також може бути деяка перевага енергії притягання, якій відповідає вторинний неглибокий мінімум (друга потенціальна яма), глибина якого може змінюватися від 0 до (5-10) kT В залежності від співвідношення між енергіями притягання і відштовхування можливі різні типи потенційних кривих сумарної взаємодії між частинками (рис.57,б).
Рис. 57. Залежність потенційної кривої від відстані між частинками.
Крива 1 відповідає такому стану системи, коли на будь – яких відстанях між частинками переважає енергія притягання, і відповідає швидкій коагуляції. Крива 2 відповідає оборотній коагуляції – флокуляції. Частинки, що злипаються залишаться розділеними прошарком рідкого середовища. Крива 3 відповідає системі, яка має високий потенційний бар’єр і є агрегативно стійкою. Крива 4 відповідає системі в якій концентрація електроліту дорівнює порогу коагуляції. Проаналізуємо криву 4, рис.57, в точці екстремуму виконуються дві умови: US=0; dUS/dh = 0 (7.10) В цьому випадку для частинок з малим потенціалом одержуємо
cкр, hкр - критичні значення, що відповідають мові (7.10) Похідна від енергії взаємодії по h
Розділимо отриманий вираз на попередній і отримаємо cкр = 2/hкр (7.13) Підставимо цей вираз в рівняння (7.11) отримаємо:
При малих значеннях потенціалу поверхні поріг швидкої коагуляції відповідає певному співвідношенню між потенціалом поверхні і товщиною дифузійного шару ПЕШ. Якщо співвідношення Згідно теорії ДЛФО коагуляція, що відбувається в наслідок зменшення потенціалу частинок, називається нейтралізаційною, а внаслідок стискання дифузійного шару - концентраційною. Нейтралізаційна коагуляція характерна для систем з малим електричним потенціалом поверхні. Протиіони, адсорбуючись в поверхневому шарі, зменшують заряд частинки майже до нуля, в результаті чого відбувається коагуляція. В цьому випадку при введенні в колоїдний розчин достатньо великої кількості електроліту дисперсна система може перейти в другу область стійкості в якій частинки будуть мати протилежний за знаком заряд. Підставимо вираз (7.14) в рівняння для розрахунку товщини дифузійного шару (5.24):
При нейтралізаційній коагуляції критична концентрація електроліту залежить від потенціалу частинки і обернено пропорційна квадрату заряду іона. Для частинок з великім потенціалом збільшення концентрації індиферентного електроліту приводить до зменшення товщини дифузійного шару, в наслідок чого відбувається концентраційна коагуляція. Для частинок з великим значенням потенціалу поверхні енергія взаємодії між частинками практично не залежить від значення потенціалу поверхні (7.8), умова стійкості до коагуляції визначається товщиною дифузійного шару і критичною концентрацією електроліту.
Похідна від (7.17) по h:
Поділимо рівняння (7.17) на (7.18) і одержимо вираз ідентичний виразу (7.13). Підставимо (7.13) в (7.17) та виведемо значення критичної концентрації концентраційної коагуляції:
Якщо підставити (7.19) в рівняння для розрахунку товщини дифузійного шару (5.24), то одержимо: скр =const/z6 (7.20) Критична концентрація концентраційної коагуляції обернено пропорційна заряду іона в шостому степені. с1:с2:с3 = (1/1)6:(1/2)6:(1/3)6 = 1:(1/64):(1/726) У 1882 р. Шульце встановив, що коагулююча здатність іонів (1/скр) зростає з ростом їх валентності. Ця залежність була підтверджена Гарді і отримала назву правила коагуляції Шульце –Гарді, або правила значності. Крім того у 1900 р. Гарді встановив, що коагулюючу дію мають тільки іони з протилежним до колоїдної частинки знаком заряду. Для золю As2S3 Шульце експериментально знайшов наступні співвідношення коагулюючої сили одно-, дво- та тривалентних іонів: 1 20:350; Фрейндліх для такого ж золю і тих самих катіонів встановив наступні співвідношення: 1:7:531; Піктон і Лінгер встановили такі значення: 1:20:1500. Розходження між значеннями що одержані різними авторами можна пояснити тим, що важко одержати колоїдні систем з однаковими характеристиками. Подальші досліди показали, що коагулюючи сила іонів однакової валентності зростає з ростом їх іонного радіуса.
Приклад 7.1 Розрахуйте енергію взаємодії сферичних частинок діаметром 200 нм у водному розчині NaCl, якщо потенціал φδ = 20 мВ, константа Гамакера = 0,5∙10-19 Дж, параметр æ= 1∙108 м-1, температура Т = 293 К, відносна діелектрична проникність середовища ε = 81, а відстань між поверхнями частинок h = 2нм. Згідно з теорією стійкості ДЛФО для слабозаряджених поверхонь (φδ<25 мВ) загальна енергія взаємодії між двома частинками U складається з енергії електростатичного відштовхування Ue і енергії Ван-дер-Ваальсівського притягання Uв. U = Ue + Uв = 2π r ε ε0 φδ2 ln(1 - e-æx) – Ar / 12 h = = 2 ∙ 3,14 ∙1∙10-7∙ 81∙8,85∙10-12 ∙ (0,02)2 ∙ln(1 + е-0,2) - - 0,5∙10-19∙1∙107 / 12 ∙2∙10-9 = 10,77 ∙10-20 – 20,83∙10-20 Дж = = -10,06∙10-20 Дж. На відстані 2нм переважає енергія Ван-дер-Ваальсівського притягання.
|



 (7.7)
(7.7) (7.8)
(7.8) (7.9)
(7.9)
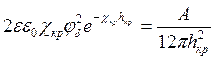 (7.11)
(7.11) (7.12)
(7.12) , або (7.14)
, або (7.14) більше за константу В, то система агрегативно стійка, якщо менше, то відбувається коагуляція. Ця умова була сформульована Ейлерсом і Корфом у 1940р.
більше за константу В, то система агрегативно стійка, якщо менше, то відбувається коагуляція. Ця умова була сформульована Ейлерсом і Корфом у 1940р.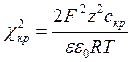 (7.15)
(7.15)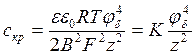 (7.16)
(7.16)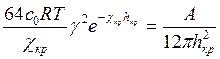 (7.17)
(7.17)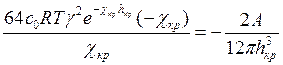 (7.18)
(7.18) (7.19)
(7.19)


