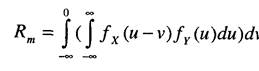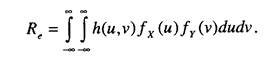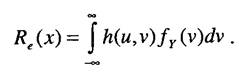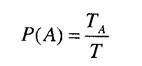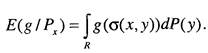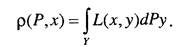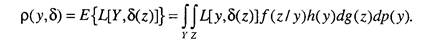Выбор как максимизация критерия 2 страница

• при принятии решения необходимо исключить любой риск, т.е. ни при каких условиях не допускается получать результат, меньший чем

13.4. Концепция риска в задачах системного анализа

Допущение пусть даже малой вероятности а принятия ошибочного решения не исключает возможности риска. Полное устранение риска при принятии решений практически даже и не требуется; мало того, определенная степень риска вводится сознательно, так как принятие решения без риска, например, с предельно пессимистической позиции, как правило, невыгодно. Однако при этом разумный риск следует отличать от риска азартного игрока. Любой риск, во-первых, должен учитываться по возможности полно, описываться количественными характеристиками и ограничиваться, а во-вторых, ни в коем случае не превышать уровень, при котором результат достигается с достаточной надежностью. В качестве опорного для оценки риска принимается решение, получаемое на основании минимаксного критерия, так как данное решение соответствует позиции крайней осторожности.

В литературе встречается различное понимание термина «риск» и в него иногда вкладывают довольно сильно отличающиеся друг от друга трактовки. Однако общим во всех этих представлениях является то, что под риском понимают неуверенность, произойдет ли нежелательное событие и возникнет ли неблагоприятное состояние. Проблемы риска, тем не менее, часто приходится решать, и выбор варианта решения в общем случае, так или иначе, связан с риском. Поэтому попытаемся найти такое определение риска, которое в достаточной степени соответствовало бы содержанию рассматриваемых задач и в то же время отвечало бы общей концепции теории принятия решений.

С понятием риска часто связывается представление о возможных или грозящих событиях с катастрофическими последствиями и потерями. Отсюда следует точка зрения, что такого события следует избежать любой ценой. При ожидаемых потерях, связанных с жизнью и здоровьем, это представление выражено особенно резко, и оно ясно формулируется в соответствующих инструкциях, например по технике безопасности. Конечно, нужно четко сказать, что полностью свободной от риска техники, несмотря на самые большие затраты, не существует. Однако техническим задачам далеко не всегда сопутствуют такие отягчающие обстоятельства. Ущерб вследствие решения, принятого с учетом риска, может оказаться ничтожно малым по сравнению с затратами на то, чтобы избежать такого ущерба. Учитывая необходимость количественных оценок, можно предложить следующую формулировку понятия риска: величина риска, связанная с реализацией нежелательного события или состояния, есть произведение величины последствий реализации события на меру возможности его наступления.

Обозначим через А некоторое нежелательное событие или состояние, которое может произойти. Пусть данное событие характеризуется некоторой вероятностью наступления Р(А) и некоторыми последствиями U(A). Тогда риск, связанный с наступлением события Л, будет определяться следующим образом:

R(A) = ЩА) Р(А).

Последствие в принципе нежелательного события или состояния может в соответствии со своей величиной описываться и оцениваться специфическими параметрами. Диапазон при этом весьма широк - от экономических до этических ценностей. Мерой возможности наступления события служит вероятность q его наступления.

При угрозе материальным ценностям степень риска измеряют в денежном выражении. Если различные последствия нежелательного

события одинаковы или очень велики, то для сравнения достаточно рассматривать одни соответствующие вероятности. Наряду с этим может быть угроза ценностям, которую нельзя выразить количественно, например, когда последствия события нельзя предусмотреть достаточно полно. Примером могут служить последствия выхода из строя прибора, используемого в различных областях народного хозяйства, которые поставщик оценить не может. В этом случае мерой риска остается принять вероятность превышения предела нагрузки. При риске, связанном со здоровьем, последствия могут быть частично оценены количественно в таких категориях, как простой в работе или расходы на оплату подменяющего персонала и т.п. При риске, связанном с летальным исходом, количественные оценки последствий в большинстве случаев отсутствуют. При существовании угрозы жизни люди в настоящее время почти всегда, тем не менее, работают. Особые проблемы возникают в случаях, когда опасность грозит и людям, и материальным ценностям одновременно, и желательно меру такого риска сравнить с другими рисками. Риск может быть явно связан с факторами, не поддающимися учету. Так, эстетический вред, наносимый построенным сооружением уникальному ландшафту, практически невозможно оценить.

Заключительная оценка риска бывает проста, когда имеют дело только с угрозой материальным ценностям, а возможный ущерб выражен количественно. При угрозе материальным ценностям и невозможности количественно выразить возможный ущерб нужно этот ущерб оценить приблизительно и продолжать рассмотрение, мирясь с таким недостатком информации. Поскольку нецелесообразно идти на сколь угодно большие затраты, чтобы устранить риск полностью, нужно оценить угрозу людям. Субъективные оценки сильно отклоняются от известных частот реализации тех или иных нежелательных событий. Значения риска субъективно привлекательной деятельности обычно занижаются. Риск события, на которое оценивающему трудно или невозможно оказать влияние, наоборот, обычно переоценивается. Риск события катастрофического характера, как правило, тоже получает более высокую оценку. Кроме того, субъективные оценки меняются со временем. В результате из-за этих некорректностей субъективные оценки не могут быть положены в основу технических решений.

Сравнение рассматриваемой рискованной ситуации с возникавшими в прошлом аналогичными ситуациями дает для оценки риска более надежные исходные данные. Проблема оценки этим, однако, все же не решается. В отдельных случаях, конечно, можно довольствоваться требованием, чтобы допустимый риск был заведомо ниже имевшего место в аналогичных ситуациях ранее. Но в других случаях, особенно при очень высоком уровне затрат, проблема остается нерешенной. Требование четко ограничить допустимые вероятности реализации нежелательного события наталкивается на препятствия, обусловленные следующими положениями:

• такого рода границы должны быть независимыми от экономических затрат, но аналогичная независимость должна существовать также для угрозы безопасности людей и материальным ценностям;

• лицо, принимающее решения, должно для подобных границ принимать общее решение, учитывающее всю специфику частных случаев;

• одно лишь утверждение, что такие границы будут соблюдаться, может освободить лицо, принимающее решение, от обязанности анализировать ситуацию дальше и направлять свои усилия на дальнейшее снижение угрозы безопасности людей. При этом возможны случаи, когда ценой очень небольших затрат опасность может быть еще больше снижена, а этим пренебрегают, поскольку границы уже установлены;

• утверждение, что выдерживаются определенные границы, предполагает качественное единство данных, что на самом деле недостижимо, так как имеют место проблемы самого различного типа;

• ограничения допустимого риска зависят от времени и меняются с изменениями технических и экономических возможностей общества.

Угроза безопасности людей чаще всего состоит из многих составляющих риска, например, из основного существующего риска, риска вследствие ошибок и риска, на который идут сознательно при известных условиях.

Любой математический алгоритм оценки риска должен исходить из того, что твердо установлен экономический эквивалент угрозы. Этот эквивалент должен быть обоснован в том смысле, что он соответствует затратам, которые общество при данных условиях может себе позволить, чтобы предотвратить или уменьшить угрозу. Необходимо воспрепятствовать тому, чтобы, с одной стороны, ценой больших затрат был уменьшен и без того незначительный риск, а с другой - чтобы оставался большой риск, который может быть устранен с небольшими затратами. Установить такой эквивалент - еще не значит добиться успеха. И при многоцелевых решениях эквивалент такого типа не удается получить без влияния субъективных факторов. Тем не менее, эти эквиваленты делают более ясным риск при принятии решения и помогают лучше определить ответственность за выполненную оценку. Решения, связанные с риском, всегда остаются для исследователя сомнительными, так как нельзя заранее определить затраты для четкого разделения во всех случаях оправданного и неоправданного риска. Проконтролировать, был ли оправдан данный риск, удается всегда только после наступления нежелательного события, и возможно это только при оправданных убытках.

Примеры формирования риска в задачах системных исследований

Технический риск. Технические объекты подвергаются опасности при возрастании нагрузки. Если при этом будет превзойден предел (например, прочности), произойдет выход объекта из строя. В данном частном случае под риском целесообразно понимать вероятность наступления определенного сочетания неблагоприятных событий. Риск целесообразно описывать вероятностью при следующих условиях:

а) если последствия выхода из строя объекта нельзя выразить экономическими показателями;

б) если экономические соображения играют подчиненную роль;

в) если экономические последствия важны, но не поддаются количественной оценке;

г) если последствия столь велики, что без особых рассуждений нужно минимизировать вероятность выхода объекта из строя.

Технический риск характеризуется, таким образом, вероятностью превышения предела. Если X и 7- случайные переменные, причем X характеризует нагрузку, a 7- несущую способность, то для технического риска справедливо соотношение

R_m=p{X>Y).

Если существуют плотности распределения нагрузки и несущей способности fjx) и/у(у), то при независимости X и 7 можно записать

Если, кроме того, известна зависимость плотностей распределения от временных, t) uf_y(y, t), то получим

Зависимость плотности распределения нагрузки от времени отражает характер воздействия факторов во времени на исследуемый объект. Зависимость плотности распределения несущей способности от времени отражает процессы старения в самом исследуемом объекте.

Таким образом, задача определения технического риска сводится к определению плотностей распределения нагрузки и несущей способности.

Технико-экономический риск. В данном пункте рассмотрим случай, когда последствия при конкретных нагрузке X и несущей способности Y можно описать функцией h(x, у). На первый взгляд кажется важным рассмотреть критический случай, когда х > у, т.е. когда уровень нагрузки превышает несущую способность. Это условие можно было бы выразить в виде h(x, у) = 0 для х < у и однозначно оценить критический случай х>у простым утверждением, что при этом h(x,y) = \. Однако реальные данные из практики показывают, что первые признаки разрушения появляются еще до достижения нагрузкой несущей способности, и, наоборот, в других случаях, при нагрузке, превышающей несущую способность, объект продолжает функционировать. Так что ограничение функции h(x, у) всего двумя значениями 0 и 1 может оказаться слишком грубым описанием. Определим технико-экономический риск R_e при независимости нагрузки X и несущей способности Уи известных ^плотностях распределения fjx) и/_у(у) ожидаемых случайных величин следующим соотношением:

Для определенного данного значения х нагрузки условное математическое ожидание риска равно

Угроза безопасности людей. Если при анализе безопасности технических объектов существуют события А., при достижении которых возникает угроза здоровью обслуживающего персонала, описываемая количественно функцией потерь h(A), то для описания функции риска можно пользоваться выражениями, аналогичными тем, которые были получены для технико-экономического риска. Если функцию потерь сформировать не удается, то в качестве меры риска допустимо использовать вероятность наступления нежелательного события, как это было сделано в случае технического риска. Дополнительно следует, однако, рассмотреть еще ряд возможных случаев.

Угроза при эксплуатации технических средств определяется двумя категориями влияний - событиями, представляющими угрозу, и попаданием в опасную зону. События, представляющие угрозу, и попадание в опасную зону - явления случайные. В предположении равномерности распределения событий во времени можно получить следующие выражения для вероятности наступления события, представляющего угрозу:

и для вероятности попадания в опасную зону:

То есть вероятности выражаются как отношения интервалов времени. Здесь приняты следующие обозначения: Т_А - суммарная продолжительность события, представляющего угрозу; Т_Е - продолжительность пребывания в опасной зоне; Т - рассматриваемый интервал времени, для которого принимается решение.

Если событие А, представляющее угрозу, и пребывание в опасной зоне Е независимы, то вероятность совместной реализации этих двух событий можно оценить по формуле

Р(АпЕ) = Р(А)Р(Е).

Эта формула говорит, что при данных значениях Р(А) и Р{Е) следует считаться с вероятностью совпадения опасностей, т.е. одновременного наступления представляющего угрозу события и попадания в опасную зону в рассматриваемый отрезок времени. Однако отсюда не следует, с какой вероятностью нужно ожидать реализации по меньшей мере одной угрозы. Поэтому при использовании величины как вероятности угрозы возможны серьезные ошибки в интерпретации рассматриваемых ситуаций.

13.5. Принятие решений в условиях стохастической неопределенности

При решении вопросов системных исследований, таких как проектирование автоматизированных систем, организация их эксплуатации и т.п. возникает большое количество задач, в основе которых лежат вероятностные модели объектов или процессов, описывающих исследуемые явления. Примерами таких задач являются задачи оценивания параметров эффективности и надежности технических средств, прогнозирование поведения параметров системы, задачи, связанные с контролем работоспособности и диагностикой неисправностей при функционировании систем и отдельных компонентов, задачи организации оптимального обслуживания технических средств, задачи обоснования срока службы отдельных элементов, узлов, подсистем. В большинстве случаев существуют естественные вероятностные модели, отражающие реальный ход процессов динамического поведения объектов. Эти модели строятся на основе математических, физических или технических закономерностей, отражающих функционирование отдельных объектов, воздействие объектов друг на друга. В ряде случаев для построения вероятностной модели используется объективная информация о поведении объектов в процессе эксплуатации. По результатам обработки этой информации с помощью специальных методов математической статистики производят построение зависимостей. Например, существующие методы проверки статистических гипотез позволяют обоснованно подойти к выбору закона распределения некоторой случайной величины на основании реализовавшихся значений.

И, наконец, существуют ситуации, когда построение вероятностной модели происходит субъективно, на основании интуиции и опыта системного аналитика. При построении вероятностной модели на основании субъективной информации необходимо тщательно анализировать комбинации состояний динамических объектов, возможность появления критических ситуаций, степень вероятности ситуаций. Необходимо также привлекать информацию о сходных процессах, результатах приближенных расчетов.

Следует заметить, что при построении вероятностных моделей процессов предпочтение следует отдавать моделям, учитывающим объективные данные. Субъективные оценки необходимо применять, когда отсутствуют возможности для получения объективных данных. Однако в некоторых задачах учет субъективных вероятностей наряду с объективной информацией бывает весьма полезным. При формировании субъективных вероятностей исследователь должен постараться выразить вероятности рассматриваемых событий через вероятности более простых явлений, которые либо являются заданными, либо поддаются объективной оценке или вычислению.

Общей чертой всех подобных задач является необходимость выбора на основании косвенных или прямых, но обязательно «зашумленных» данных. Основным предположением для формализации решения задач такого типа является предположение о вероятностном характере экспериментальных данных.

Методологической основой для решения задач выбора в такой постановке является теория оптимальных статистических решений. В основе данной теории лежит понятие статистической функции риска.

Рассмотрим постановку задачи. Будем считать заданным вероятностное распределение Р на множестве возможных исходов Y, причем значение Р(у) определено для каждого исхода у. Предположим, что системный аналитик, не зная результата развития системы, должен принять решение, последствия которого зависят от этого результата (исхода). Пусть X множество всех возможных решений, которые может принять исследователь. Положим, что в результате выбора решения х и реализации исхода у исследователь получает доход г, принадлежащий пространству всех возможных доходов R. Понятие «доход» обычно определяют через полезность, которая служит для численного выражения предпочтений лица, принимающего решения.

Элементы множества R, которые названы доходами, могут быть весьма сложными объектами. Приведем примеры: множество билетов на различные концерты; множество возможных экономических состояний фирмы в определенный момент времени в будущем, измеряемых разностью ее денежных доходов в будущем и в настоящий момент; множество экономических состояний государства и т.д.

Рассмотрим пример, иллюстрирующий понятие дохода в задачах системных исследований. Пусть решается задача выбора варианта реализации структуры сложной системы. Группа проектировщиков должна принять решение о выборе одного варианта реализации системы управления из нескольких рассматриваемых. В качестве множества доходов, получаемых от реализации того или иного варианта, могут служить денежные доходы, получаемые в результате внедрения системы выработки и принятия управляющих воздействий с использованием конкретного варианта структуры системы по сравнению с традиционным способом управления. Под доходом может также пониматься длительность обработки запросов пользователей; длительность обработки результатов функционирования отдельных подразделений, например цехов; точность и достоверность выводов, полученных в результате реализации управляющих воздействий и т.д. Совокупность всех этих составляющих образует вектор дохода конкретного варианта реализации структуры системы.

Для любого множества R у системного аналитика будут предпочтения к тем или иным доходам. В некоторых ситуациях эти предпочтения очевидны. Например, в случае денежных доходов, чем больше доход, тем он предпочтительнее.

Сложнее сформулировать предпочтение в случае, когда доход -векторная величина. При сравнении двух векторных доходов, если каждая компонента первого вектора представляется более желательной, нежели соответствующая компонента второго вектора, то предпочтение отдается первому вектору. Если первый выгоднее только в отношении некоторых своих компонент, в то время как второй вектор предпочтительнее по другим компонентам, то какому из этих векторов отдать предпочтение, не очевидно. Для окончательного решения вопроса следовало бы приписать соответствующие веса отдельным компонентам.

При сравнении двух доходов г, е R и r₂ e R пишут г_у<г_г, если г₂ предпочтительнее r_v и г, = г₂, если г_х эквивалентен г₂, т.е. имеет место одинаковая выгодность. Если г_х не является более предпочтительным, чем r_v то пишут г, < г,.

Предполагается, что на основе своих предпочтений среди доходов системный аналитик может задать полное упорядочение множества R. Другими словами налагаются следующие условия.

1. Если г, и г₂ - произвольные доходы из множества R, то верно одно и только одно из следующих соотношений:

2. Если г,, г₂ и г_ъ - доходы из R, причем г, < г₂ и г, < г_ъ, то г_{ < г_у Наконец, будем предполагать, что не все доходы в R эквивалентны

между собой, т.е. исключается тривиальная ситуация, а именно, предполагается, что s₀ -< t₀ хотя бы для одной пары s₀ e R, t_Qe R.

В большинстве задач аналитик не вполне свободен в выборе дохода. Обычно он может лишь выбрать из некоторого класса возможных распределений вероятностное распределение на R, согласно которому будет определен его доход.

Например, ставится вопрос о выборе определенного технологического процесса из двух или более возможных таких процессов. Хотя доходы и можно точно выразить через производительность и издержки, производственные характеристики различных процессов могут быть описаны лишь вероятностью.

Другой пример. Системный аналитик хочет получить информацию о значении некоторого параметра. Его доход - это количество информации об этом значении, получаемое после эксперимента. Пусть он выбирает эксперимент из некоторого класса доступных ему, но информация, которую он получит в каждом из экспериментов, носит случайный характер. В любой задаче такого рода аналитик производит выбор не непосредственно среди доходов из множества R, а среди вероятностных распределений на R.

Вероятностное распределение на множестве доходов задают в том случае, когда величина, определяющая доход, имеет характер непрерывной случайной величины. Так, в задаче выбора определенного технологического процесса из нескольких возможных вариантов для каж-

дого процесса могут быть известны средние характеристики. Однако в реальной эксплуатации характеристики технологического процесса могут изменяться в широких пределах. На них оказывает влияние ряд факторов, таких как наличие ресурсов для стабильной работы предприятия, психологический климат в коллективе, состояние здоровья работников, занятых в данном производстве и т.п. Таким образом, доход, получаемый от реализации конкретного варианта технологического процесса, будет величиной случайной, зависящей от большого количества факторов.

То же можно сказать и в случае решения задачи выбора варианта структуры системы управления. Допустим, что проектные документы гарантируют некоторые характеристики качества функционирования системы, такие как быстродействие системы, объем информации, передаваемой по каналам связи, объемы памяти и т.д. Но необходимо отдавать отчет в том, что эти характеристики являются средними. Они могут существенно меняться в зависимости от характеристик конкретных технических средств, например, характеристик надежности. Так, частые отказы одной системы приводят к снижению характеристик качества, в то время как надежная работа другой системы позволяет поддерживать ее характеристики качества на достаточно высоком уровне. В данном случае вектор дохода, получаемого от эксплуатации системы, будет величиной случайной, зависящей от вероятности безотказной работы технических средств (впрочем, как и от ряда других факторов).

Функции полезности.

Таким образом, величина дохода, получаемого от реализации того или иного варианта решения, является случайной величиной, зависящей от различных факторов. В случае благоприятного стечения факторов можно получить максимальный доход от выбора определенной альтернативы. В случае неблагоприятного стечения факторов получают минимальный доход. Естественно, что будет некоторое количество промежуточных доходов, зависящих от вероятности реализации того или иного набора факторов.

Поскольку доходы могут иметь различное выражение (денежное выражение дохода, быстродействие системы, объем памяти и т.п.) необходимо обеспечить возможность их сравнения. Как было указано ранее нужно иметь систему предпочтений, систему весовых коэффициентов, с помощью которых можно было бы производить сравнение вариантов реализации различных альтернатив, когда они описываются векторными системами доходов. В качестве такой системы предпочтений выступает функция полезности. Для всякого распределения Ре Хи всякой вещественной функции q на множестве R обозначим через E{glP) математическое ожидание функции q (если оно существует) относительно распределения Р. Другими словами

Вещественная функция g, заданная на множестве R, называется функцией полезности, а для любого дохода г е R число g(r) называется полезностью г. Для всякого распределения Р е 9? число E(g/P) называ-¹ ют полезностью Р или средней полезностью.

Определение функции потерь

Рассмотрим теперь пространство X всех возможных решений х, а R пространство всех возможных доходов г, которые может получить исследователь в результате решения х и исхода у. Доход из R, получаемый исследователем при решении х и исходе у обозначим через о(х, у). Будем считать заданным вероятностное распределение Р на пространстве исходов Y, причем значение Р(у) определено для каждого исхода у. Предположим также, что на множестве R задана функция полезности.

Для всякого вероятностного распределения Р_х, для которого функ-ция g интегрируема, среднюю полезность E{glP) можно вычислить по формуле

Тогда задача исследователя будет состоять в выборе решения х, максимизирующего E{glP).

В задачах принятия решения каждому доходу г е R принято сопоставлять не полезность, а потери. Функция потерь определяется равенством

L(x, у) = -g(o(x, у)).

При любом (х,у) число L(x,y) представляет собой ущерб исследователя от принятия решения х, в случае, когда реализовался исход у. Пусть Р - вероятностное распределение исхода у. При всяком решении х средний ущерб р(Р, х) называется риском и определяется по формуле

В этом случае системный аналитик должен стремиться к выбору решения х, минимизирующего риск р(Р, х). Таким образом, сформировано правило выбора решения в случае, когда на пространстве исходов задано распределение вероятностей.

Задачи решения с наблюдениями

Рассмотрим задачи решения, в которых исследователь перед тем как выбрать решение из множества X, наблюдает значение случайной величины или случайного вектора z, связанного с исходом у. Наблюдение z дает исследователю некоторую информацию о значении у, которая помогает ему принять рациональное решение. Будем полагать, что для всех у е Y задано условное распределение z.

Поскольку решение исследователя зависит от наблюдаемого значения z, он должен выбрать решающую функцию 8, задающую для любого возможного значения z & Z решение 8(z) e X. В этом случае функция риска будет определяться равенством

Термин «риск» здесь как и ранее относится к среднему ущербу. Для каждого решения х е Хр(у, 5) обозначает риск от принятия решения х. Распределение h(y) называется априорным, так как оно задает распределение у до проведения наблюдения над z.

Цена наблюдения

В задачах принятия решений наблюдение случайной величины z связано с определенными затратами, которые должны учитываться аналитиками, проводящими системные исследования, при расчете риска от принятия решающей функции, использующей результаты наблюдения z. Это обстоятельство играет особенно важную роль в случае, когда аналитику надо решить, какую из нескольких случайных величин предпочтительнее наблюдать, или ответить на вопрос, производить ли наблюдения вообще. Пусть с(у, z) обозначает цену наблюдения значения z из множества Z. Тогда, если h(y) есть априорная плотность распределения случайной величины у, то средняя цена наблюдения равна