DC Electricity
Coursework 15
1. a) A current of 1.0 A flows through a wire whose cross-sectional area is 1 mm2. The free electron density is 5.0 × 1028 m-3. What is the drift velocity of the electrons? b) The current is now trebled and the diameter of the wire doubled. By what factor is the drift velocity multiplied as a result? (4 marks)
2. a) State – in one sentence - Ohm’s law. You want to design a circuit using resistors of resistance 10 kΩ, 15 kΩ and 22 kΩ. b) Show, by calculation, how two of these resistors could be connected to produce an effective resistance of 6 kΩ. c) Determine the largest effective resistance achievable with these three resistors. d) Show, by calculation, how all three resistors could be connected to produce an effective resistance of 28 kΩ. e) Determine how the engineer could connect these resistors to a 6V battery with negligible internal resistance so that the current taken from the battery is 1.27 mA.
(10 marks)
3. Four resistors are connected as shown:
Between which two points is the resistance a maximum? What is the maximum resistance? (4 marks)
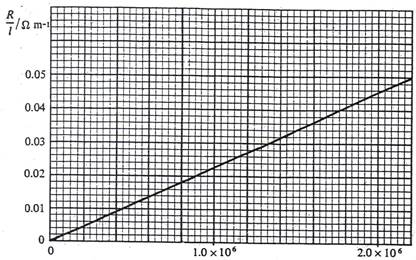
4. The graph below shows the results of an experiment designed to investigate how the resistance per unit length, (R/l), of different gauges of copper wire varies with diameter, d, of the wire.
1/d2 (m-2)
a) (i) Write down a relationship connecting (R/l) with diameter, d, of the wire. (ii) Then determine the resistivity of copper. b) A copper cable that is 10 m long is used to supply power to a 3 kW immersion heater operating from a 240 V mains supply. (i) What approximately is the current through the cable when the heater is switched on? (ii) If the diameter of the copper core used is 1.78 mm, use the graph to determine the resistance of the connecting cable needed to carry the current. (iii) How much power is dissipated in the cable while the heater is switched on? (iv) State two reasons why thinner wire is unsuitable for the copper core. (12 marks)
5. a) Redraw the circuit shown below with an ammeter included, positioned so that it shows the current passing through only the 5 Ω resistor.
b) What will the reading on the ammeter be? c) What power will be dissipated in the 5 Ω resistor? (6 marks)
6. A cell of negligible internal resistance is connected in series with a microammeter of negligible resistance and two resistors whose resistances are 15 kΩ and 30 kΩ. The current is 200 μA. a) Calculate the e.m.f. of the cell. b) When a voltmeter is connected in parallel with the 15 kΩ resistor, the current in the microammeter increases to 250 μA. Sketch a diagram of the modified circuit and calculate the resistance of the voltmeter. (8 marks)
7. a) Define – in a sentence – the term capacitance. b) An isolated conducting sphere of radius 1.00 cm is supported by a fine insulating thread and charged to a high potential, V, relative to Earth with an electrostatic device. Calculate the capacitance of this sphere.
c) A 22nF capacitor is connected in parallel with a high resistance voltmeter as shown above. The voltmeter reads zero. The small conducting sphere, already charged, is brought into contact with the point P. Show that:
d) The voltmeter now reads 1.5V. Calculate: (i) the charge transferred to the 22nF capacitor (ii) the initial potential, V, of the small conducting sphere (
8. A thundercloud has a horizontal lower surface area of 2 km2 and is 750 m above the earth. a) Treating the arrangement as a capacitor, calculate the electrical energy stored when its potential is 105 V above the earth. b) If the cloud rises to 1250 m, what change in electrical energy occurs? (8 marks)
9. Determine the voltage across and the charge stored in each of the capacitors shown in the circuit below.
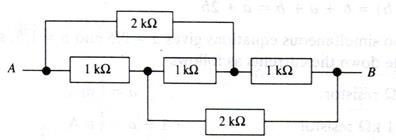
10. A current of 1 mA enters the resistor network shown at A and leaves at B. Find the current in each resistor.
(10 marks)
|




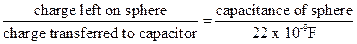
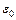 has its usual value). (10 marks)
has its usual value). (10 marks)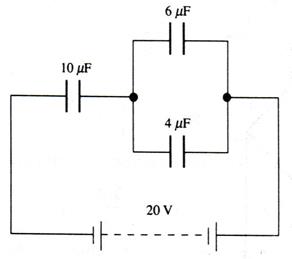 (4 marks)
(4 marks)