Генерация плазмы при внешней ионизации
L8 Газовый диод с накаленным катодом
На предыдущей лекции рассматривались различные способы увеличения тока через диод при компенсации электронного заряда ионным. Ионы эмитировались анодом либо плазмой, создаваемой некоторым генератором. При наличии в промежутке газа, можно, вообще говоря, осуществить генерацию плазмы непосредственно в нем. Генерация плазмы при внешней ионизации Рассмотрим модельную задачу о генерации плазмы при инжекции в промежуток длиной d, на который подано напряжение U, электронного потока с плотностью тока j0 и энергией w0 =ej0 (соответственно скоростью v0 = ne=ni=n (1) ne =
В качестве граничных условий взяты следующие
Интегрируя (3) и учитывая (1) и (2) получим
Подставляя в (4) вместо G производную потока из (3) и используя (1) можно преобразовать (4) к следующему виду
Наконец подставляя (2) и (3’) в (4’) получаем дифференциальное уравнение для потенциала
Интегрируя по dx от 0 до х, получаем
где введен параметр
и Преобразуя (5) получим явное аналитическое выражение для распределения потенциала в промежутке
Чтобы выполнилось второе граничное условие для потенциала (
Тогда, вспоминая, каким образом был введен параметр а, получаем
откуда для искомого уровня ионизации находим
Соответственно для плотности тока ионной эмиссии из генерируемой плазмы получаем выражение
При уровне ионизации меньшем, чем это определяется выражением (10), генерируемых ионов недостаточно для установления квазинейтрального состояния во всем промежутке, но возможно возникновения такого состояния в некоторой части промежутка. В остальной части будет преобладать электронный заряд. При превышении ионизацией уровня, определяемого выражением (10) мы можем ожидать преобладания в промежутке ионного заряда и возникновения немонотонного распределения потенциала с максимумом. В последнем случае заряд вторичных электронов, скорей всего, должен учитываться, так как они будут захватываться в потенциальную яму, формируемую ионами.
Дуговой разряд
Это разряд с невысоким напряжением горения ~ потенциала ионизации, горящий в газонаполненных промежутках, но со сравнительно невысоким давлением, и поддерживаемый благодаря высокой температуре катода, при которой из него возможно осуществление эффективной термоэмиссии. Если нагрев катода обеспечивается тем или иным вспомогательным устройством, то такой разряд очевидно является несамостоятельным. При большом токе разряда возможен переход в самостоятельный режим, в котором высокая Т катода обеспечивается за счет бомбадировки катода ионами. Переход в самостоятельный режим мы обсудим в конце лекции а сначала поговорим о зажигании несамостоятельного разряда и его характеристиках. 1. Поджиг разряда. Несмотря на разогрев катода и поступление в промежуток термоэлектронов этого еще недостаточно для зажигания разряда. При достаточно низком давлении наполняющего газа эмиттированные электроны будут уходить на анод практически не взаимодействуя с атомами газа в режиме свободного полета. Протекание тока через такой непробитый не заполненный ионизованным газом промежуток вполне можно описать используя закон 3/2 для вакуумного диода J0 = Записанная формула определяет предельный пропускаемый через промежуток ток, его пропускную способность. Именно такой ток и будет протекать, если эмиссионная способность термокатода Je =AT2 exp(-B/Т) превышает j0. Избыточные электроны будут отталкиваться полем объемного электронного заряда обратно в катод. Если je<j0, то все эмитированные электроны достигнут анода. тогда j=je. При повышении давления электроны на своем пути к аноду производят ионизацию и промежуток заполняется плазмой, в которой электрическое поле невелико, а практически весь перепад потенциала сосредоточен в катодном слое, в котором навстречу друг другу движутся поток термоэмитированных электронов и ионный поток из плазмы. Сравнивая характерный вид распределения потенциала в вакуумном промежутке, где преобладает отрицательный заряд, и в дуге, где преобладает положительный заряд, логично считать границей между ними случай, когда отрицательный и положительный заряды примерно равны между собой и рассматривать условие qi=qe как критерий зажигания разряда. Рассмотрим качественно при каких давлениях газа выполнение этого условия становится возможным. Для выполнения записанного условия вовсе необязательно чтобы каждый электрон осуществил ионизацию. Учитывая, что скорость движения ионов существенно меньше, в
где si - сечение ионизации, усредненное по промежутку. Преобразуя записанное соотношение получим оценку величины критического давления, при котором зажигается разряд р=kTg Учитывая, что усредненное сечение не может быть больше максимального сечения ионизации, получим оценку снизу для критического давления газа, при котором становится возможным зажигание дуги рcr > kTg при d = 1 cм = 0.01 м В оценочную формулу (1) не входит напряжение, поданное на промежуток, но понятно что с уменьшением этой величины уменьшается si и, соответственно, критическое р будет возрастать с уменьшением напряжения. Однако обычно дугу зажигают не путем увеличения давления при некотором заданном напряжении, а путем повышения напряжения при некотором заданном давлении. В этом случае говорят о напряжении зажигания. Получим связь Uзаж(р) используя следующие соображения. Предположим, что распределение потенциала является линейным j(x) = (x /d)U, т.е. будем считать, что не только qi=qe, но и плотности зарядов ri= re в любой точке промежука одинаковы. Кроме того будем считать, что напряжение незнaчительно превышает порог ионизации. В этом случае si = с(e - ei ) = ce(j (x) - ji ) Тогда <si >= где xi = jid/U - точка в которой энергия электронов достигает порога ионизации. Переходя от интегрирования по х к интегрированию по j получим <si>= Подставляя полученное выражение в (1) и вводя безразмерные переменные h = U/ji, y = (M/m)1/2 cejipd/kT получим следующее уравнение 2h/у =(h-1)2 Раскрывая скобки, деля на 2 и группируя слагаемые получаем следующее квадратное уравнение
Решение квадратного уравнения дает зависимость h(у), т.е. фактически зависимость Uзаж(р) h = 1 + 1/у + ((1+1/у)2 - 1)1/2 Знак + перед квадратным корнем выбран из физических соображений, т.к. ясно, что потенциал зажигания должен быть больше ji или в безразмерных переменных h > 1. Функция h(у) монотонно падает и при больших у, т.е. при повышении давления стремится к 1. Качественно полученная кривая согласуется с экспериментом и результатами более точных расчетов. Следует обратить внимание на проблему выбора критерия поджига. В ряде работ в качестве такого критерия выбирается условие обращения Е в 0 на аноде. Интегрируя уравнение Пуассона с граничным условием Ек=0 можно показать, что такое условие (Еа=0) соответствует условию qi=qe. Считается, что при выполнении такого условия вблизи анода зарождается плазма, которая затем распространяется к катоду. Но, по-видимому наиболее правильным является расчет ВАХ диода и выявление точки в которой dU/dj меняет знак. Соответственно в этой точке dj/dU обращается в бесконечность. Результаты точных расчетов, которые проводились с использованием кинетического уравнения показывают, что это происходит еще до того, как напряженность электрического поля на аноде обратится в 0. Эти результаты подтверждают сделанные предположения, что распределение потенциала близко к линейному (исключением очевидно является область непосредственно вблизи катода где Е=0, но здесь ионизация еще не идет, поэтому это не сильно влияет на проведенные оценки), и что поджиг происходит приблизительно когда отношение электронного и ионного тока достигает величины (M/m)1/2. Характеристики разряда. После зажигания поле сосредотачивается в прикатодном слое толщиной L, а остальное пространство заполнено плазмой, на которой перепад потенциала незначителен. Величина тока, который может пропустить такой промежуток существенно выше, чем для вакуумного промежутка, но тем не менее при высокой температуре катода, вполне возможно, что ток разряда будет меньше тока эмиссии Id<Ie. Такой режим работы называют свободным. При выполнении обратного условия Id>Ie режим называется несвободным. Реализация того или иного режима может быть достигнута путем варьирования температуры катода, ЭДС источника питания и сопротивления балластного резистора R. Нетрудно сообразить, что реализции например свободного режима способствовало бы увеличение Т и R и уменьшение ЭДС. Впрочем что касается увеличения R и уменьшения ЭДС, то здесь не следует слишком увлекаться, т.к. можно и перестараться и погасить разряд вернув его в режим характерный для вакуумного диода. Рассмотрим характеристики катодного слоя ДНК в обоих указанных режимах. Свободный режим катода. В этом случае напряженность поля на катоде Ек=0. Если быть более точным то на самом деле вблизи катода имеется минимум потенциала, отражающий избыточные электроны, которые вылетают из катода, имея некоторую скорость. и Е = 0 в точке минимума, но как и при рассмотрении задачи о вакуумном диоде сделаем упрощающее предположение и положим Ек=0 и v=0 при х=0. На другой границе катодного слоя КС где начинается плазма со слабым электрическим полем также можно принять Е(L)=0 и положить скорость ионов, входящих в слой из плазмы, также равной 0, vi(L) =0. Для нахождения ВАХ КС необходимо решить ур-ние Пуассона, в правой части которого в отличие от случая вакуумного диода появится ионный заряд.
где rе = je/ve = je/(2ej/m)1/2, ri = ji/vi = ji/(2e(Uc-j)/M)1/2 Введем безразмерные переменные у = j/Uc, z = x/L, и параметр b = и перепишем ур-ние Пуассона в следующем виде
где j0 - ток электронов через вакуумный промежуток толщиной L и с падением напряжения Uс. Умножая на dy/dz и интегрируя по dz от 0 до z получим
Учитывая что dy/dz = 0 при y = 1 получаем, что b должно равняться 1. Это означает, что ji = (m/M)1/2 je, т.е. ji << je и следовательно jd
Разделяя переменные и интегрируя от 0 до 1 получим
Интеграл в правой части берется численно и после подстановки полученного значения и возведения в квадрат получается je/j0=1.861. Таким образом мы получили связь между плотностью тока в катодном слое напряжением на нем и длиной прикатодного слоя, поскольку j0 связана с Uс и L. Но для получения вольт-амперной характеристики необходимо определить L. Если принять что все ионы образованные в плазме, т.е. на участке длиной d-L поступают в катодный слой, то получаем ji = ce(Uc-ji)N(d-L)je (1) С другой стороны ji = (m/M)1/2 je (2) Сравнивая записанные соотношения получим L = d - Окончательно для ВАХ получаем
Поскольку перепад потенциала на плазме мал, то Ud ce(Uc-ji)Nd = (m/M)1/2 Следовательно Uc = ji + Мы получили ВАХ используя простейшие предположения. Обсудим возможность их применения и возможные уточнения. Сделанное предположение о том, что все ионы достигают КС скорей всего применимо, когда продольный размер промежутка d существенно меньше поперечных размеров. Если это не так, то значительная доля ионов может например уйти на стенки камеры. В таком случае вводится коэффициент s зависящий от геометрии системы и давления и показывающий какая доля от полного ионного тока Ii попадает в КС Iкc = sIi В свою очередь для нахождения Ii вводится к-т a, характеризующий полную ионизацию газа, отнесенную к току пучка электронов a = Ii/Ie. Записанное нами ранее соотношение для ионизации в плазме справедливо лишь при самых низких давлениях, когда большая часть электронов пролетает промежуток в бесстолкновительном режиме и лишь незначительная доля успевает испытать ионизирующее столкновение. При более высоких давлениях, когда пробег << d практически все электроны успевают провзаимодействовать и растратить свою энергию. В этих условиях к-т a перестает зависеть от геометрии и давления, но конечно зависит от начальной энергии электронов, а также от рода газа. Что касается КС то его толщина незначительна и в нем предположение о свободном пролете частиц справедливо в широком диапазоне условий. Однако с увеличением ионизации и увеличением ионного тока поступающего в КС из плазмы температура катода может оказаться недостаточной для того чтобы обеспечить эмиссию из катода электронного тока превосходящего ионный в (M/m)1/2 раз. Тогда как уже отмечалось катод начинает работать в несвободном режиме.
Несвободный режим. В этом случае Ек уже отлична от 0, но на границе плазмы по-прежнему можно принять Е = 0. Введенный к-т b=(je/ji)(m/M)1/2 будет равен b = Само уравнение Пуассона не изменится
где rе=je/ve=je/(2ej/m)1/2, ri=ji/vi=ji/(2e(Uc-j)/M)1/2 Используя те же безразмерные переменные у=j/Uc, z=x/L, перепишем ур-ние Пуассона в несколько ином виде
где через j0 теперь обозначен ток ионов через вакуумный промежуток толщиной L и с падением напряжения Uс. Умножая на dy/dz и интегрируя по dz от z до 1 получим
Умножая на 2 и извлекая квадратный корень получаем
Чтобы выражение под корнем было положительным при у=0 необходимо, чтобы b изменялось от 0 до 1. b не может быть отрицательным по своему физическому смыслу, а при b=1 происходит переход к свободному режиму. Разделяя переменные и интегрируя от 0 до 1 получим
В отличие от ранее рассмотренного случая подинтегральное выражение содержит параметр b и интеграл будет не просто каким-то числом, а некоторой функцией от b. Функции F и k затабулированы. Тогда ji= k(b)j0 je=bk(b)j0(M/m)1/2 Мы опять же получили связь тока с напряжением и длиной слоя, хотя поступление ионов из плазмы уже учтено. В данном случае для исключения L и получения ВАХ необходимо определить поле на катоде и воспользоваться выражениями для автотермоэлектронной эмиссии. Ограничимся вычислением поля. Подставляя в (3) у=0 получим для безразмерной переменной
Используя полученное выражение для ji и возвращаясь к размерным переменным получим Ек = Ясно, что в несвободном режиме для увеличения тока понадобится увеличение Ек и соответственно напряжения на промежутке. Эксперимент. В целом результаты экспериментов подтверждают выявленные закономерности. При очень низких давлениях характеристика мало отличается от вакуумного промежутка. При повышении давления до значений ~ 10-3 становится возможным зажигание разряда, причем напряжение зажигания уменьшается по мере увеличения р. После зажигания на ВАХ появляется падающий участок, затем ток растет практически без изменения напряжения на промежутке, хотя ЭДС источника питания конечно приходится повышать. Промежуток заполнен светящейся плазмой, за исключением тонкого темного прикатодного слоя толщиной ~ 0.1 мм. После того как ток разряда достигнет тока эмиссии, то для дальнейшего роста тока необходимо увеличение напряжения. При давлениях ~ 0.1 - 1 Торр при достаточно высокой температуре катода при увеличении тока в свободном режиме возможен переход к так называемой низковольтной дуге, напряжение горения которой даже меньше, чем потенциал ионизации. Зондовые измерения показывают, что в этом случае в промежутке распределение потенциала является немонотонным, имеется максимум, в котором j больше потенциала ионизации, а плазма оказывается неоднородной. В этом режиме, по-видимому, существенна ступенчатая ионизация атомов. Для низковольтной дуги также характерен практически постоянный уровень напряжения, который сменяется ростом U после достижения током разряда тока эмиссии. Отметим еще один интересный экспериментальный результат, явно не укладывающийся в рамки рассмотренной модели. При давлениях ~ 0.01-1 Торр и плотности разрядного тока > 0.1 А/см2 в парах ртути и в инертных газах за исключением неона наблюдалось образование на некотором расстоянии от КС еще одного темного слоя толщиной ~ нескольких мм, который называют вторым или рассеивающим. С понижением давления этот слой исчезает, а затем превращается в ярко светящийся слой тех же размеров. В зависимости от напряжения горения слой может светиться слабее или сильнее плазмы и менять окраску. Теория рассеивающего слоя разработана слабо. Переход в самостоятельный режим. Как и при пониженных давлениях с повышением тока наступает момент, когда ток разряда сравнивается по величине с током эмиссии и происходит переход в несвободный режим и повышение напряжения. По мере увеличения тока и напряжения увеличивается энергия приносимая на катод ионами. В результате температура катода начинает повышаться и термоэмиссия усиливается. Рост напряжения замедляется и при достижении некоторого тока начинается уменьшение напряжения. На этом участке ВАХ нагрев катода от вспомогательного нагревателя уже перестает играть существенную роль. Нагрев катода до высокой Т может быть обеспечен благодаря ионной бомбардировке, а накальная цепь может быть отключена. Таким образом происходит переход к самостоятельной дуге с накаленным катодом. Tемпературу до которой разогревается катод в результате ионной бомбардировки можно оценить приняв, что энергия приносимая ионами на катод рассеивается в результате излучения. jiUc = sT4 Это допущение справедливо если можно пренебречь теплоотводом вглубь катода.
|

 ). В промежутке также идет равномерная ионизация G под действием внешнего источника. Попробуем определить при какой интенсивности внешней ионизации в промежутке возникнет квазинейтральное состояние. Пренебрегая вкладом в полный отрицательный заряд электронов, образовавшихся в промежутке, по сравнению с вкладом инжектированных электронов запишем систему уравнений для рассматриваемой ситуации.
). В промежутке также идет равномерная ионизация G под действием внешнего источника. Попробуем определить при какой интенсивности внешней ионизации в промежутке возникнет квазинейтральное состояние. Пренебрегая вкладом в полный отрицательный заряд электронов, образовавшихся в промежутке, по сравнению с вкладом инжектированных электронов запишем систему уравнений для рассматриваемой ситуации. (2)
(2) (3)
(3)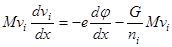 (4)
(4) ,
,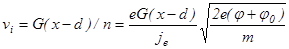 (3’)
(3’)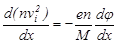 (4’)
(4’)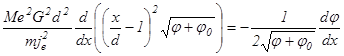 (4’’)
(4’’)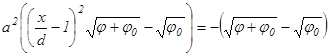 (5)
(5)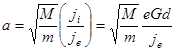 , (6)
, (6) - плотность ионного тока на катоде
- плотность ионного тока на катоде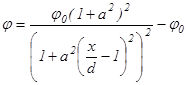 (7)
(7)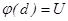 ) параметр а должен иметь некоторое определенное значение, а именно
) параметр а должен иметь некоторое определенное значение, а именно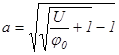 (8)
(8)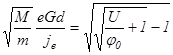 , (9)
, (9) (10)
(10) (11)
(11)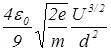 .
.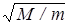 раз, достаточно чтобы плотность ионного тока составляла соответствующую долю от электронной плотности тока. Таким образом должно выполняться следующее условие
раз, достаточно чтобы плотность ионного тока составляла соответствующую долю от электронной плотности тока. Таким образом должно выполняться следующее условие /sid (1)
/sid (1)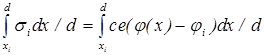


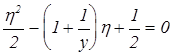


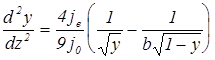

 je. Умножая на 2 и извлекая квадратный корень получаем
je. Умножая на 2 и извлекая квадратный корень получаем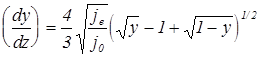

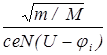

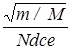 .
.


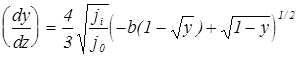 (3)
(3)
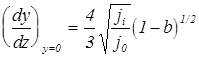
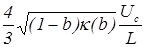 .
.


