Обзор обучения
Целью обучения сети является такая подстройка ее весов, чтобы приложение некоторого множества входов приводило к требуемому множеству выходов. Для краткости эти множества входов и выходов будут называться векторами. При обучении предполагается, что для каждого входного вектора существует парный ему целевой вектор, задающий требуемый выход. Вместе они называются обучающей парой. Как правило, сеть обучается на многих парах. Например, входная часть обучающей пары может состоять из набора нулей и единиц, представляющего двоичный образ некоторой буквы алфавита. На рис. 3.4 показано множество входов для буквы «А», нанесенной на сетке. Если через квадрат проходит линия, то соответствующий нейронный вход равен единице, в противном случае он равен нулю. Выход может быть числом, представляющим букву «А», или другим набором из нулей и единиц, который может быть использован для получения выходного образа. При необходимости распознавать с помощью сети все буквы алфавита, потребовалось бы 26 обучающих пар. Такая группа обучающих пар называется обучающим множеством.
Рис. 3.4. Распознавание изображении Перед началом обучения всем весам должны быть присвоены небольшие начальные значения, выбранные случайным образом. Это гарантирует, что в сети не произойдет насыщения большими значениями весов, и предотвращает ряд других патологических случаев. Например, если всем весам придать одинаковые начальные значения, а для требуемого функционирования нужны неравные значения, то сеть не сможет обучиться. Обучение сети обратного распространения требует выполнения следующих операций: 1. Выбрать очередную обучающую пару из обучающего множества; подать входной вектор на вход сети. 2. Вычислить выход сети. 3. Вычислить разность между выходом сети и требуемым выходом (целевым вектором обучающей пары). 4. Подкорректировать веса сети так, чтобы минимизировать ошибку. 5. Повторять шаги с 1 по 4 для каждого вектора обучающего множества до тех пор, пока ошибка на всем множестве не достигнет приемлемого уровня. Операции, выполняемые шагами 1 и 2, сходны с теми, которые выполняются при функционировании уже обученной сети, т. е. подается входной вектор и вычисляется получающийся выход. Вычисления выполняются послойно. На рис. 3.3 сначала вычисляются выходы нейронов слоя j, затем они используются в качестве входов слоя k, вычисляются выходы нейронов слоя k, которые и образуют выходной вектор сети. На шаге 3 каждый из выходов сети, которые на рис. 3.3 обозначены OUT, вычитается из соответствующей компоненты целевого вектора, чтобы получить ошибку. Эта ошибка используется на шаге 4 для коррекции весов сети, причем знак и величина изменений весов определяются алгоритмом обучения (см. ниже). После достаточного числа повторений этих четырех шагов разность между действительными выходами и целевыми выходами должна уменьшиться до приемлемой величины, при этом говорят, что сеть обучилась. Теперь сеть используется для распознавания и веса не изменяются. На шаги 1 и 2 можно смотреть как на «проход вперед», так как сигнал распространяется по сети от входа к выходу. Шаги 3, 4 составляют «обратный проход», здесь вычисляемый сигнал ошибки распространяется обратно по сети и используется для подстройки весов. Эти два прохода теперь будут детализированы и выражены в более математической форме. Проход вперед. Шаги 1 и 2 могут быть выражены в векторной форме следующим образом: подается входной вектор Х и на выходе получается вектор Y. Векторная пара вход-цель Х и Т берется из обучающего множества. Вычисления проводятся над вектором X, чтобы получить выходной вектор Y. Как мы видели, вычисления в многослойных сетях выполняются слой за слоем, начиная с ближайшего к входу слоя. Величина NET каждого нейрона первого слоя вычисляется как взвешенная сумма входов нейрона. Затем активационная функция F «сжимает» NET и дает величину OUT для каждого нейрона в этом слое. Когда множество выходов слоя получено, оно является входным множеством для следующего слоя. Процесс повторяется слой за слоем, пока не будет получено заключительное множество выходов сети. Этот процесс может быть выражен в сжатой форме с помощью векторной нотации. Веса между нейронами могут рассматриваться как матрица W. Например, вес от нейрона 8 в слое 2 к нейрону 5 слоя 3 обозначается w 8,5. Тогда NET-вектор слоя N может быть выражен не как сумма произведений, а как произведение Х и W. В векторном обозначении N = XW. Покомпонентным применением функции F к NET-вектору N получается выходной вектор О. Таким образом, для данного слоя вычислительный процесс описывается следующим выражением: О = F (XW). (3.3) Выходной вектор одного слоя является входным вектором для следующего, поэтому вычисление выходов последнего слоя требует применения уравнения (3.3) к каждому слою от входа сети к ее выходу. Обратный проход. Подстройка весов выходного слоя. Так как для каждого нейрона выходного слоя задано целевое значение, то подстройка весов легко осуществляется с использованием модифицированного дельта-правила из гл. 2. Внутренние слои называют «скрытыми слоями», для их выходов не имеется целевых значений для сравнения. Поэтому обучение усложняется. На рис. 3.5 показан процесс обучения для одного веса от нейрона р в скрытом слое j к нейрону q в выходном слое k. Выход нейрона слоя k, вычитаясь из целевого значения (Target), дает сигнал ошибки. Он умножается на производную сжимающей функции [OUT(1 – OUT)], вычисленную для этого нейрона слоя k, давая, таким образом, величину δ. δ = OUT(1 – OUT)(Target – OUT) (3.4) Затем δ умножается на величину OUT нейрона j, из которого выходит рассматриваемый вес. Это произведение в свою очередь умножается на коэффициент скорости обучения η (обычно от 0,01 до 1,0), и результат прибавляется к весу. Такая же процедура выполняется для каждого веса от нейрона скрытого слоя к нейрону в выходном слое. Следующие уравнения иллюстрируют это вычисление: Δ w pq,k = η δq,k OUT (3.5) w pq,k(n+1) = w pq,k(n) + Δ w pq,k (3.6) где w pq,k(n) – величина веса от нейрона p в скрытом слое к нейрону q в выходном слое на шаге n (до коррекции); отметим, что индекс k относится к слою, в котором заканчивается данный вес, т. е., согласно принятому в этой книге соглашению, с которым он объединен; w pq,k(n+1) – величина веса на шаге n + 1 (после коррекции); δq,k – величина δ для нейрона q, в выходном слое k; OUTp,j – величина OUT для нейрона р в скрытом слое j.
Рис. 3.5. Настройка веса в выходном слое Подстройка весов скрытого слоя. Рассмотрим один нейрон в скрытом слое, предшествующем выходному слою. При проходе вперед этот нейрон передает свой выходной сигнал нейронам в выходном слое через соединяющие их веса. Во время обучения эти веса функционируют в обратном порядке, пропуская величину δ от выходного слоя назад к скрытому слою. Каждый из этих весов умножается на величину δ нейрона, к которому он присоединен в выходном слое. Величина δ, необходимая для нейрона скрытого слоя, получается суммированием всех таких произведений и умножением на производную сжимающей функции:
(см. рис. 3.6). Когда значение δ получено, веса, питающие первый скрытый уровень, могут быть подкорректированы с помощью уравнений (3.5) и (3.6), где индексы модифицируются в соответствии со слоем.
Рис. 3.6. Настройка веса в скрытом слое .Для каждого нейрона в данном скрытом слое должно быть вычислено δ и подстроены все веса, ассоциированные с этим слоем. Этот процесс повторяется слой за слоем по направлению к входу, пока все веса не будут подкорректированы. С помощью векторных обозначений операция обратного распространения ошибки может быть записана значительно компактнее. Обозначим множество величин δ выходного слоя через D k и множество весов выходного слоя как массив W k. Чтобы получить D j, δ-вектор выходного слоя, достаточно следующих двух операций: 1. Умножить о-вектор выходного слоя D k на транспонированную матрицу весов W’ k, соединяющую скрытый уровень с выходным уровнем. 2. Умножить каждую компоненту полученного произведения на производную сжимающей функции соответствующего нейрона в скрытом слое. В символьной записи D j = D k W’ k $ [ 0 j $ (I – 0 j)], (3.8) где оператор $ в данной книге обозначает покомпонентное произведение векторов, О j – выходной вектор слоя j и I – вектор, все компоненты которого равны 1. Добавление нейронного смещения. Во многих случаях желательно наделять каждый нейрон обучаемым смещением. Это позволяет сдвигать начало отсчета логистической функции, давая эффект, аналогичный подстройке порога персептронного нейрона, и приводит к ускорению процесса обучения. Эта возможность может быть легко введена в обучающий алгоритм с помощью добавляемого к каждому нейрону веса, присоединенного к +1. Этот вес обучается так же, как и все остальные веса, за исключением того, что подаваемый на него сигнал всегда равен +1, а не выходу нейрона предыдущего слоя. Импульс. В работе [7] описан метод ускорения обучения для алгоритма обратного распространения, увеличивающий также устойчивость процесса. Этот метод, названный импульсом, заключается в добавлении к коррекции веса члена, пропорционального величине предыдущего изменения веса. Как только происходит коррекция, она «запоминается» и служит для модификации всех последующих коррекций. Уравнения коррекции модифицируются следующим образом: Δ w pq,k(n+1)= η δq,k OUTp,j + aΔ w pq,k(n) (3.9) w pq,k(n+1) = w pq,k(n) + Δ w pq,k(n+1) (3.10) где (a – коэффициент импульса, обычно устанавливается около 0,9. Используя метод импульса, сеть стремится идти по дну узких оврагов поверхности ошибки (если таковые имеются), а не двигаться от склона к склону. Этот метод, по-видимому, хорошо работает на некоторых задачах, но дает слабый или даже отрицательный эффект на других. В работе [8] описан сходный метод, основанный на экспоненциальном сглаживании, который может иметь преимущество в ряде приложений. Δ w pq,k(n+1)= (1-a) δq,k OUTp,j + aΔ w pq,k(n) (3.9) Затем вычисляется изменение веса w pq,k(n+1) = w pq,k(n) + ηΔ w pq,k(n+1), (3.10) где a коэффициент сглаживания, варьируемый и диапазоне от 0,0 до 1,0. Если a равен 1,0, то новая коррекция игнорируется и повторяется предыдущая. В области между 0 и 1 коррекция веса сглаживается величиной, пропорциональной a. По-прежнему, η является коэффициентом скорости обучения, служащим для управления средней величиной изменения веса.
|



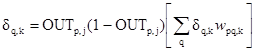 (3.7)
(3.7)



