Движение жидкости в рабочем колесе. Треугольники скоростей. Уравнение Эйлера.
Абс.ск.движения жидк.на входе – С1, на выходе из раб.к. абс.ск.ув, обознач. С2 Абс.ск.движ.жидк.равна геометрич.сумме относительной ск.в колесе и окружной ск.вращения колеса:
U-вектор окружн.ск.,касат.к окружности ω-вектор относит.ск.,касат.к окружности β2-угол между относит.ск.и касат.к лопатке C2-вектор абс.ск.на выходе из раб.колеса α2-между абс.ск.и касат.к окружности C2r-радиальная составляющая абс.ск C2u-окружная составляющая абс.ск.
Напор, развиваемый раб.к.,центроб.машины зависит от ск.потока проходящего ч/з раб.к. и от его р-ров. Эту связь устанавливает ур-ие Эйлера: H=
|
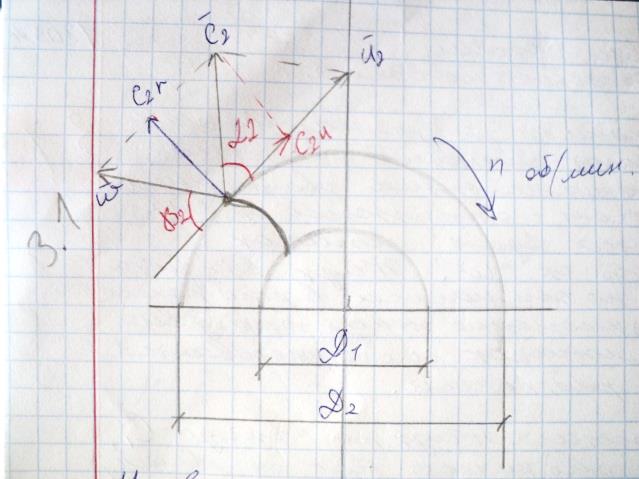Проходя ч/з каналы раб.к.частицы жидк.совершают сложные движения. На ряду с вращательным движением вместе с колесом с окружной ск.U жидк.двигается вдоль лопаток с относительной ск ω. Жидк.входит в раб.к.по оси насоса,в раб.к. происходит отклонение жидк., она двигается вдоль лопаток и отбрасывается к перифирии раб.к.
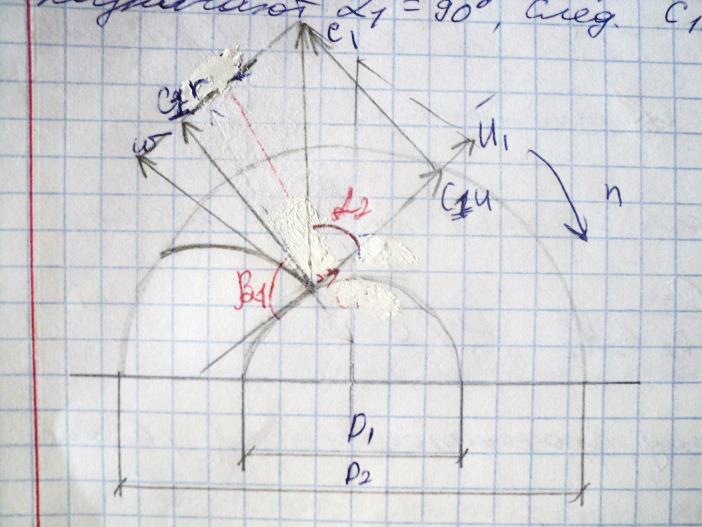С=U+ ω
м.вод.ст.
