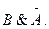Алгоритм анализа переключательной схемы
1. Записать логическую формулу, соответствующую данной переключательной схеме. 2. По полученной формуле построить таблицу истинности. 3. Выбрать в таблице истинности наборы (строки), где функция принимает единичные значения. Единицы в рассматриваемых наборах соответствуют замкнутым переключателям, а нули — разомкнутым. Пример 2. Проанализируем переключательную схему из предыдущего примера. 1. 2.
3. Электрическая цепь пропускает ток, если состояния переключателей соответствуют наборам: 0001, 0011, 0101, 0110, 0111, 1001, 1010, 1011, 1101, 1110, 1111. Синтез переключательной схемы — это разработка схемы, условия работы которой заданы таблицей истинности или словесным описанием. Пример. Построим схему электрической цепи, включающей переключатели А, В, С, такую, что цепь замыкается лишь в том случае, если замкнуты все переключатели или ни один из этих переключателей. Решение. Оформим в виде таблицы все возможные соположения переключателей А, В, С и в отдельном столбце отметим требуемое состояние для каждого набора состояний переключателей:
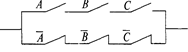
Построим СДНФ: F(A,B,C)=A & B & C V A & B & С. Этой логической функции соответствует переключательная схема:
Упрощение (минимизация) переключательной схемы сводится к упрощению соответствующей ей формулы на основании законов алгебры логики. Пример. Упростить схему:
Решение. Исходная схема имеет девять переключателей.
Рассматриваемая схема может быть заменена более простой, содержащей только три включателя
5.8. Использование алгебры логики в вычислительной технике
При разработке вычислительной техники широкое применение находит алгебра логики. Любая информация может быть представлена дискретным сигналом — в виде фиксированного набора отдельных значений. Устройства, в которых действуют такие сигналы, называются дискретными. Всякий преобразователь информации — некая искусственная система обработки информации, устройство, имеющее входы и выходы. Простейшими преобразователями информации являются логические преобразователи дискретного действия. Их условное обозначение:
Здесь А1, А 2 ,..., Аn — входы, X1, Х 2 ,..., Хn — выходы.
На каждый вход подаются сигналы только двух видов, обозначаемые 0 и 1. Такие же сигналы появляются на каждом выходе.
5.9. Логические элементы
Дискретный преобразователь, который выдает после обработки двоичных сигналов значение одной из логических операций, называется логическим элементом. Ниже приведены условные обозначения (схемы) логических элементов, реализующих логическое умножение, логическое сложение и отрицание.
Логический элемент И (конъюнктор) реализует операцию -логического умножения. Единица на выходе этого элемента будет только тогда, когда на всех входах будут единицы. Если хотя бы на одном входе будет нуль, на выходе также будет нуль. Логический элемент ИЛИ (дизъюнктор) реализует операцию логического сложения. Если хотя бы на одном входе будет единица, то на выходе элемента также будет единица. Знак 1 на схеме элемента — остаток устаревшего обозначения операции ИЛИ (результат операции ИЛИ равен единице, если сумма значений операндов больше или равна 1). Логический элемент НЕ (инвертор) реализует операцию отрицания. Если на входе элемента нуль, то на выходе единица; если на входе элемента единица, то на выходе нуль. Описанные логические элементы могут быть реализованы многими способами — на пневматической, гидравлической, механической или электрической основе. Важно лишь, чтобы нули и единицы на входе были идентичны нулям и единицам на выходе. Любой преобразователь информации, имеющий п входов и т выходов, можно заменить набором из т преобразователей, Следовательно, для построения произвольного преобразователя информации достаточно уметь синтезировать преобразователи с одним выходом.
5.10. Комбинационные схемы
Схему преобразователя информации, сигнал на выходе которой однозначно определяется комбинацией сигналов на входах, называют комбинационной. Однотипность сигналов на входах и выходах позволяет подавать сигнал, вырабатываемый одним элементом, на вход другого элемента. Это позволяет из двухвходовых схем И и ИЛИ строить многовходовые схемы, а также синтезировать произвольные комбинационные схемы, соединяя в цепочки отдельные логические элементы. Пример 1. Покажем, как из двухвходовых схем И можно построить схему И с любым количеством входов.
Анализируя комбинационную схему, можно понять, как работает логическое устройство. Пример 2. Проанализируем комбинационную схему, т. е. выясним, какой сигнал должен быть на выходе при каждом возможном наборе сигналов на входе.
Заполненная таблица истинности полностью описывает рассматриваемую комбинационную схему. Другая форма описания логических устройств — структурная формула. Пример 3. По заданной комбинационной схеме выпишем структурную формулу.
Пример 4. По структурной формуле вычертим соответствующую комбинационную схему:
Решение. Нам потребуются два инвертора, два конъюнктора и один дизъюнктор.
|


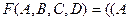 Ú
Ú  Ú
Ú 

 Ú
Ú 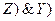 Ú
Ú  Ú
Ú 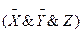 =
=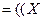 Ú
Ú  Ú
Ú  Ú
Ú 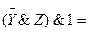
 Ú
Ú  Ú
Ú 
 Ú
Ú 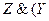 Ú
Ú  Ú
Ú  Ú
Ú 






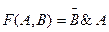 Ú
Ú