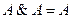Чтение и анализ переключательных схем
Прочитать переключательную схему — это значит определить, протекает по ней ток или нет при определенных состояниях переключателей. Пример. Дана схема:
Состояния переключателей задаются таблицей:
Требуется прочитать переключательную схему — заполнить колонку «Состояние схемы». Будем последовательно рассматривать все строки таблицы, описывающие состояние переключателей данной схемы. 1. Переключатели А и В разомкнуты, С замкнут. В этом случае ток не может проходить ни по одной из двух цепочек параллельного соединения. Состояние схемы 0. 2. Так как переключатель А замкнут, ток будет проходить по верхней цепочке параллельного соединения. Состояние схемы 1. 3. Ток может проходить по обеим цепочкам параллельного соединения. Состояние схемы 1. Две схемы, содержащие одни и те же переключатели А, В,..., мы будем считатьодинаковыми или равными, если при одном и том же состоянии переключателей (А замкнут, В разомкнут и т. д.) обе схемы одновременно пропускают или не пропускают ток. Естественно считать из двух схем более простой ту, которая содержит меньше переключателей. В алгебре «переключательных схем» выполняются все законы алгебры логики. В этом достаточно просто убедиться, если прочитать приведенные ниже схемы и сравнить столбец состояния каждой схемы с результирующим столбцом таблицы истинности для соответствующей логической формулы. Справедливость коммутативного закона для параллельного и последовательного соединения контактов видна на рис. 1, ассоциативного закона — на рис. 2.
Равенство схем, приведенных на рис. 3 и 4, говорит о справедливости дистрибутивного закона.
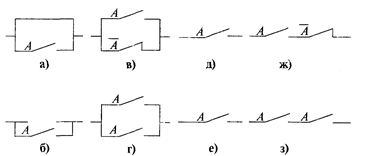
На рис. 5 приведены переключательные схемы, реализующие следующие соотношения: a) б)
|

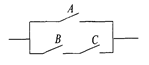

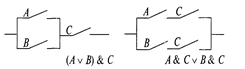

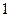 Ú
Ú  в)
в)  Ú
Ú 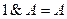 ж)
ж) 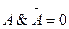
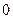 Ú
Ú  г)
г) 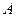 Ú
Ú 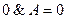 з)
з)