Составить закон распределения вероятностей числа появлений события А в трех независимых испытаниях, если вероятность появления события в каждом испытании равна 0,6.
Монета бросается 4 раза. Построить многоугольник распределения случайной величины Х- числа выпадений герба. 8. Из колоды карт (их 36) вытаскивают наудачу 5 карт. Какова вероятность того, что будет вытащены 2 туза и 3 шестерки? 9. Из букв разрезной азбуки составлено слово СТАТИСТИКА. Какова вероятность того, что, перемешав буквы и укладывая их в ряд по одной (наудачу), получим слово: а) ТИСКИ; б)КИСКА; в) КИТ; г) СТАТИСТИКА? 10. Прибор содержит две микросхемы. Вероятность выхода из строя в течении 10 лет первой микросхемы равна 0,07, а второй- 0,10. Известно, что из строя вышла одна микросхема. Какова вероятность того, что вышла из строя первая микросхема? 11. В семье трое детей. Какова вероятность того, что: а) все они мальчики; б) один мальчик и две девочки. Считать вероятность рождения мальчика 0,51, а девочки- 0,49. Составить закон распределения вероятностей числа появлений события А в трех независимых испытаниях, если вероятность появления события в каждом испытании равна 0,6. 13. Семь человек рассаживаются наудачу на скамейке. Какова вероятность того, что два определенных человека будут сидеть рядом? 14. В урне 2 белых и 7 черных шаров. Из нее на удачу вынимают (без возврата) 2 шара. Какова вероятность того, что они оба будут разных цветов? 15. Из 40 экзаменационных билетов студент П выучил только 30. Каким выгоднее ему зайти на экзамен, первым или вторым? 16. Произведено 8 независимых испытаний, в каждом из которых вероятность появления события А равна 0,1. Найти вероятность того, что событие А появится хотя бы 2 раза. 17. Вероятность сдачи экзамена первым студентом равна 0,6, а вторым- 0,9. Составить ряд распределения случайной величины Х- числа студентов, успешно сдавших экзамен в случае, когда: а) экзамены пересдавать нельзя; б) экзамен можно один раз пересдать. 18. На 5 карточках разрезной азбуки изображены буквы Е,Е,Л,П,П. Ребенок случайным образом выкладывает их в ряд. Какова вероятность того, что у него получится слово ПЕПЕЛ? 19. Три орудия стреляют в цель независимо друг от друга. Вероятность попадания в цель каждого равна 0,7. Найти вероятность попадания в цель: а) только одного из орудий; б) хотя бы одного. 20. В двух ящиках имеются радиолампы. В первом ящике содержится 12 ламп, из них 1 нестандартная; во втором 10 ламп, из них 1 нестандартная. Из первого ящика наудачу взята лампа и переложена во второй. Найти вероятность того, что наудачу извлеченная из второго ящика лампа будет нестандартной. 21. В каждом из карманов (их 2) лежит по коробку спичек (по 10 спичек в коробке). При каждом закуривании карман выбирается наудачу. При очередном закуривании коробок оказался пустым. Найти вероятность того, что во втором коробке 6 спичек. 22. Игральная кость брошена 3 раза. Написать закон распределения числа появлений шестерки. 23. Из 60 вопросов, входящих в экзаменационные билеты, студент знает 50. Найти вероятность того, что среди 3-х наугад выбранных вопросов студент знает а) все вопросы; б) два вопроса. 24. Бросаются две игральные кости. Какова вероятность появления хотя бы одной шестерки? 25. Для участия в студенческих отборочных спортивных соревнованиях выделено из первой группы курса 4, из второй- 6, из третьей группы- 5 студентов. Вероятность того, что студент первой, второй и третьей группы попадет в сборную института, соответственно равны 0,9; 0,7; 0,8. Наудачу выбранный студент в итоге соревнования попал в сборную. К какой из групп вероятнее всего принадлежал этот студент? 26. Вероятность поражения стрелком мишени при одном выстреле равна 0,75. Найти вероятность того, что при 100 выстрелах мишень будет поражена: а) не менее 70 и не более 80 раз; б) не более 70 раз. 27. В урне 8 шаров, из них 5 белых, остальные- черные. Из нее вынимают наудачу 3 шара. Найти закон распределения числа белых шаров в выборке. 28. Для проведения соревнования 10 команд, среди которых 3 лидера, путем жеребьевки распределяются на 2 группы по 5 команд в каждой. Какова вероятность того, что 2 лидера попадут в одну группу, 1 лидер- в другую? 29. Из колоды карт (их 36) наугад вынимают 2 карты. Найти вероятность того, что среди них окажется хотя бы одна «дама». 30. Вероятность для изделий некоторого производства удовлетворять стандарту равна 0,96. Предлагается упрошенная схема проверки на стандартность, дающая положительный результат с вероятностью 0,98 для изделий, удовлетворяющих стандарту, а для изделий, которые не удовлетворяет стандарту, с вероятностью 0,05. Найти вероятность того, что изделие, признанное при проверке стандартным, действительно удовлетворяет стандарту. 31. Производится три независимых выстрела по цели. Вероятности попадания при разных выстрелах одинаковы и равны 0,9. Какова вероятность: А) промаха; б) одного попадания; в) двух попаданий; г) трех попаданий? 32. В денежной лотерее выпущено 100 билетов. Разыгрывается один выигрыш в 50 руб. и десять выигрышей по 1 руб. Найти закон распределения случайной величины Х- стоимости возможного выигрыша для владельца одного лотерейного билета. 31. Вероятность сдачи экзамена первым студентом равна 0.6, а вторым- 0.9. Составить ряд распределения случайной величины Х- числа студентов, успешно сдавших экзамен в случае, когда: а) экзамены пересдавать нельзя; б) экзамен можно один раз пересдать. 32. Плотность распределения случайной величины Х задана функцией 33. Производится 3 независимых выстрела по цели. Вероятность попадания при различных выстрелах одинаковы и равны 0.9. Найти математическое ожидание числа попаданий. 34. При измерении детали получаются случайные ошибки подчиненные нормальному закону с параметром 35. Оценить с помощью неравенства Чебышева вероятность того, что: а) при бросании монеты 500 раз число выпадений герба будет заключено между 200 и 300; б) при бросании 10 игральных костей сумма очков отклонится от математического ожидания меньше, чем на 8. 36. Отдел технического контроля проверяет изделия на стандартность. Вероятность того, что изделие стандартно равна 0,9. В каждой партии содержится пять изделий. Найти математическое ожидание дискретной случайной величины Х- числа партий, в каждой из которых окажется ровно четыре стандартных изделия,- если проверке подлежит 50 партий. 37. Найти дисперсию дискретной случайной величины Х-числа появлений события А в двух независимых испытаниях, если вероятности появления события в этих испытаниях одинаковы и известно, что М(Х)=0,9. 38. Дискретная случайная величина Х имеет только три возможных значения: х1,х2, и х3, причем х1<x2<x3. Вероятности того, что Х примет значения х1 и х2 соответственно равны 0,3 и 0,2. Найти закон распределения величины Х, зная ее математическое ожидание М(Х)=2,2 и дисперсию D(X)=0,76. 39. Случайная величина имеет плотность вероятностей f {x}= Найти постоянный параметр с, математическое ожидание и дисперсию. 40. Случайная величина Х распределена нормально в интервале [-c,c]. Найти P(Х>0).
41. Производятся независимые испытания с одинаковой вероятностью появления события А в каждом испытании. Найти вероятность появления события А, если дисперсия числа появлений события в трех независимых испытаниях равна 0,63. 42. Дискретная случайная величина Х имеет только два возможных значения: х1 и х2, причем х1<х2. Вероятность того, что Х примет значение х1, равна 0,2. Найти закон распределения Х зная математическое ожидание М(Х)=2,6 и среднее квадратическое отклонение равное 0,8. 43. Вероятность появления события в каждом испытании равна ¼. Используя неравенство Чебышева, оценить вероятность того, что число Х, появлений события заключено в пределах от 150 до 250, если будет произведено 800 испытаний. 44. Случайная величина Х в интервале (-3,3) задана плотностью распределения f(x)=1/( 45. Случайная величина Х распределена с плотностью: f (x)= Найти P(|Х|< 1. Игральную кость бросили 2. В четырех независимых испытаниях случайная величина 3. В 4. Даны результаты 5. Глубина моря измеряется прибором, систематическая ошибка которого равна 6. Найдите
7. В результате проведенного социологического опроса 8. Численность повторной выборки составляет
|

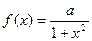 . Найти значение параметра
. Найти значение параметра 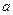 .
. мм. Производится 3 независимых измерения детали. Найти вероятность того, что ошибка хотя бы одного измерения не превосходит по модулю 2 мм.
мм. Производится 3 независимых измерения детали. Найти вероятность того, что ошибка хотя бы одного измерения не превосходит по модулю 2 мм.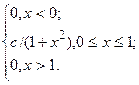
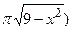 . Вне этого интервала f(x)=0. Найти дисперсию.
. Вне этого интервала f(x)=0. Найти дисперсию.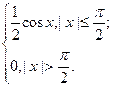
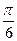 ), математическое ожидание и дисперсию.
), математическое ожидание и дисперсию. раз. При этом
раз. При этом  очко выпало
очко выпало 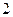 очка –
очка – 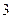 очка –
очка –  очка –
очка –  очков –
очков – 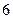 очков –
очков –  приняла следующие значения:
приняла следующие значения: 

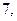
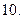 Найдите несмещенную оценку дисперсии
Найдите несмещенную оценку дисперсии 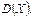
 независимых испытаниях случайная величина
независимых испытаниях случайная величина  раз, а значение
раз, а значение 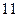 раз. Найдите несмещенную оценку дисперсии
раз. Найдите несмещенную оценку дисперсии 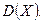
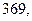



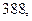

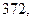
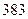 м. Найдите несмещённую оценку дисперсии ошибок измерений, если истинная длина неизвестна.
м. Найдите несмещённую оценку дисперсии ошибок измерений, если истинная длина неизвестна.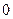 , а случайные ошибки распределены нормально со среднеквадратичным отклонением
, а случайные ошибки распределены нормально со среднеквадратичным отклонением 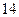 м. Каково наименьшее число независимых измерений, при котором удается определить глубину с ошибкой меньше
м. Каково наименьшее число независимых измерений, при котором удается определить глубину с ошибкой меньше 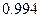 ?
? ‑доверительный интервал для генерального среднего нормально распределенного признака
‑доверительный интервал для генерального среднего нормально распределенного признака 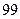 равно
равно 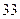 .
.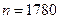 человек рейтинг кандидата в президенты составил
человек рейтинг кандидата в президенты составил 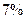 . Найдите доверительный интервал для рейтинга кандидата с гарантированной надежностью
. Найдите доверительный интервал для рейтинга кандидата с гарантированной надежностью  .
.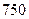 единиц. Доля признака составляет
единиц. Доля признака составляет  . Найдите с доверительной вероятностью
. Найдите с доверительной вероятностью 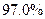 , в каких пределах находится отклонение частоты от доли признака.
, в каких пределах находится отклонение частоты от доли признака.


