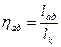Задача №1
«Цикл паросиловой установки. Цикл Ренкина». Задание: паросиловая установка работает по циклу Ренкина в двух режимах, при двух различных начальных параметрах: Р1, МПа; t1, 0C; P1`, МПа; t1`, 0C. Конечное значение давления пара – Р2, кПа для обоих вариантов одно и то же. Показать сравнительным расчетом целесообразность применения пара высоких начальных параметров, определив для обоих вариантов: 1. Термодинамический КПД установки; 2. Удельный расход пара. Изобразить: 1. Схему простейшей паросиловой установки и дать краткое описание ее работы. 2. Представить цикл Ренкина в PV и TS координатах, обозначив узловые точки в следующем порядке: 1 – 2 – изоэнтропное расширение; 2 – 3 – конденсация; 3 – 4 – нагнетание; 4 – 5 – нагревание; 5 – 6 – парообразование; 6 – 1 – перегрев. 3. Представить графическое решение задачи в is координатах. Решение: Исходные данные
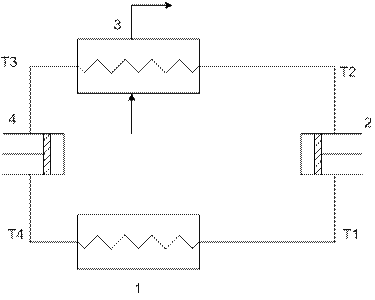
Схема простейшей паросиловой установки.
1- котел; 2- пароперегреватель; 3- турбина; 4- генератор; 5- конденсатор; 6- насос. Цикл Ренкина в PV и TS координатах.
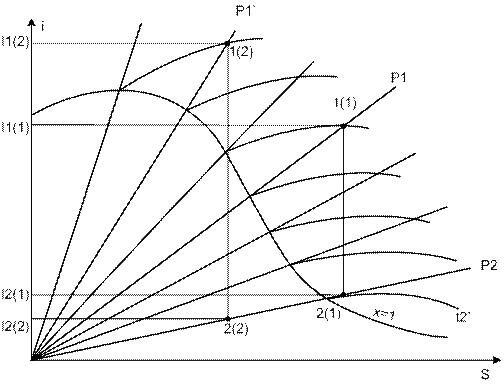
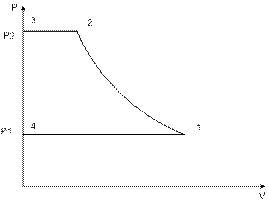
х=0 – степень сухости пара (воды); х=2 – процесс кипения (жидкость - пар); х=1 – насыщенный пар. Принцип действия (узловые точки). В паровом котле вода нагревается при Р=const до температуры насыщения. В точке 5 начинается процесс кипения. Линия 4-5 – нагрев воды. Точка 6 – насыщенный пар. Точка 1 – перегрев пара. Линия 5-6 – парообразование. Линия 2-3 – конденсация пара. Линия 3-4 – подача воды в котел. График решения задач в iS координатах.
Термодинамический коэффициент КПД установки. Линия 1-2 – полезная работа => i1(1)=3328 кДж/кг i2(1)=2216 кДж/кг i1(2)=3500 кДж/кг
i2(2)=2016 кДж/кг t2`=33 0C i2`=137.8 кДж/кг
1) 2) Удельный расход пара 1) 2) Вывод: сравнивая термодинамический коэффициент КПД и удельный расход пара, мы видим, что целесообразнее применять пар высоких начальных параметров. Контрольный вопрос: В заданиях с паром графический метод решения предпочтительнее аналитического т. к. он более нагляден и удобен. «Теплообменники». Задание: газоводяной рекуперативный теплообменник выполнен из стальных труб, где δ =4мм – толщина стенки; λ=62 Вт/(м∙К) – коэффициент теплопроводности. Греющим теплоносителем являются дымовые газы с начальной температурой tгн, 0C и конечной температурой tгк, 0C. Для расчета теплообменника в задании используются следующие величины: расход воды Мв, кг/с; начальная температура воды tвн, 0C; конечная температура воды tвк, 0C; коэффициент теплоотдачи от газов к стенке трубы αг, а от стенки трубы к воде αв. Определить: для обеих схем (прямоток и противоток) движения теплоносителей площади поверхностей теплообмена. Расчет: Схемы движения теплоносителей.
На графиках изменение температур выглядит следующим образом. Графики описывающие процесс.
Площадь теплопередающей поверхности теплообменника определяется из основной формулы теплопередачи.
Q – тепловая мощность, к – коэффициент теплопередачи; F – площадь теплопередающей поверхности; Δtср- среднеарифметический температурный напор. Тепловая мощность от греющего теплоносителя передается к нагреваемому через поверхность нагрева и вычисляется из уравнения теплового баланса. Q= Мг∙Сг∙(tгн- tгк)∙η= Мв∙Св∙(tвн- tвк), кВт η =0.8…0.95 – КПД теплообменника, Св=4.19 кДж/(кг∙К) Коэффициент к находится по формуле:
При нелинейном характере изменения температур теплоносителей, температурный напор между ними определяется, как среднелогарифмический.
Q=4.19∙2.7∙(120-16)=1176.5 кВт; к=1/(1/50+0.004/62+1/5500)=50 1)Для прямотока: Δtср=((430-16)-(140-120))/ln(414/20)=130 0C F=1176555/(50∙130)=181 м2 2)Для противотока: Δtср=((430-120)-(140-16))/ln(310/124)=202.9 0C F=1176555/(50∙202.9)=115.9 м2 Вывод: При противотоке теплообменник имеет меньшую теплопередающую поверхность. Он более выгоден, так как при одной и той же площади теплообмена противоточная схема передаст большую тепловую мощность. Контрольный вопрос: коэффициент теплопередачи – это отношение количества теплоты, преданной от одного тела к другому при разности температур между ними в один градус. Он характеризует интенсивность теплопередачи. Эта величина равна плотности теплового потока, отнесенному к температурному напору между теплоносителями.
Коэффициент теплоотдачи характеризует интенсивность теплообмена между поверхностью тела и окружающей средой. Численно он равен тепловому потоку, проходящему через 1 м2 поверхности при разнице температур между поверхностью тела и окружающей средой, равной 1К.
Задача №3 «Цикл идеального компрессора». Задание: одноступенчатый поршневой компрессор работает (сжатие) по изотерме, адиабате или политропе с показателем – к. Рассчитать цикл идеального компрессора, определив: 1. Объем в начале и в конце каждого процесса сжатия. 2. Работу цикла для каждого процесса. Изобразить: 1. Без масштаба цикл идеального компрессора с описанием всех процессов цикла в PV координатах. 2. В PV координатах рассчитанный цикл специального компрессора. 3. Индикаторную диаграмму реального одноступенчатого поршневого компрессора и схему его устройства. Решение:
Компрессор – это устройство для сжатия и перемещения газов. При движение поршня вправо открывается всасывающий клапан. Цилиндр заполняется газом. Это всасывание на индикаторной диаграмме изображено линией 4 – 1. При обратном движении поршня всасывающий клапан закрывается, и газ сжимается по линии 1 – 2. Давление в цилиндре увеличивается до тех пор, пока не станет больше Р2. Затем нагнетательный клапан открывается, и газ выталкивается в сеть(2 - 3). После этого нагнетательный клапан закрывается и процесс повторяется. На индикаторной диаграмме площадь 1-2-3-4-1 отображает работу, которую должен затратить привод компрессора. Величина этой работы при Р1=Р2 зависит от процесса сжатия 1-2. Он может идти: 1-2 по изотерме; 1-2`` по адиабате; 1-2` по политропе.
Выгоднее было бы применить изотермическое сжатие, так как уменьшается Lтех, но при этом требуется тщательное охлаждение цилиндра компрессора(применяют водяные рубашки). Практически процессы сжатия идут по политропе с показателем n=1.18…1.2. В реальных компрессорах под поршнем остается вредное пространство. При этом производительность компрессора снижается. Работа компрессора оценивается объемным КПД, который представляет собой отношение:
Линия 3-4 в реальном компрессоре реальна, так как газ во вредном пространстве перед всасыванием расширяется по линии 3-4. При расчетах вводят понятие КПД изотермического процесса:
КПД адиабатного процесса: КПД эффективный: ηэфк=ηиз∙ (ηадиаб)∙ηмех Данные для расчета.
1. Удельный объем в начале сжатия: Р1∙V1=R∙T1=>V1=R∙T1/P1=287∙345/150000=0.66 м3 2. Параметры в конце сжатия: Изотерма: P1∙V1=P2∙V2=>V2=V1∙P1/P2=0.66∙150000/700000=0.14 м3 T1=T2=345 K Адиабата: P1∙V1k=P2∙V2k=>V2=V1∙(P1/P2)1/k=0.66∙(0.15/0.7)1/1.4=0.22 м3 T2=P2∙V2/R=700000∙0.22/287=537 K Политропа: P1∙V1n=P2∙V2 n=>V2=V1∙(P1/P2)1/n=0.66∙(0.15/0.7)1/1.32=0.21 м3 T2=P2∙V2/R=700000∙0.21/287=512 K 3. Удельный объем и работа(L и l): Изотерма: l=R∙T∙ln(P2/P1)=287∙345∙ln(0.7/0.15)=152527 Дж/кг L=M∙l=2.3∙152527=350812 Дж Адиабата: l=k∙R∙(T2-T1)/(k-1)=1.4∙287∙(537-345)/(1.4-1)= 192864 Дж/кг L=M∙l= 192864∙2.3= 443587Дж Политропа: l=n∙R∙(T2-T1)/(k-1)=1.32∙287∙(512-345)/(1.4-1)=158165 Дж/кг L=M∙l=2.3∙158165=363779 Дж 4. Изменение энтропии: Изотерма: S2-S1=R∙ln(P2/P1)=287∙ln(700000/150000)=442 Дж/(кг∙К) Адиабата: S2=S1=const Политропа: S2-S1=(CV∙(n-k) ∙(n-1)) ∙ln(T2/T1)= =(1.005∙(1.32-1.4) ∙0.32) ∙ ln(512/345)=-0.01 кДж/(кг∙К) Контрольный вопрос: В одноступенчатом компрессоре при достижении Р2=0.8…1.2 МПа объем сжатого воздуха станет равным объёму вредного пространства, в результате чего весь воздух сжатый в течении этого хода компрессора останется в цилиндре и начнет расширяться вслед за возвратным ходом поршня. Второй причиной является то, что с увеличением степени сжатия возрастает температура газа в конце цикла. Для смазки цилиндров применяется масло, температура вспышки которого 200…400 0C. Т. к. разложение масла с образованием легковоспламеняющейся воздушно-масляной смеси происходит при более низких температурах, температуру сжимаемого воздуха ограничивают 160…180 0C.
Задание № 4 «Цикл воздушно-компрессорного холодильника». Задание: воздушно компрессорный холодильник холодопроизводительностью Q кВт имеет параметры состояния воздуха в узловых точках P1, t1 , Р2 . Требуется рассчитать идеальный цикл воздушно-компрессорного холодильника: 1. Определить неизвестные температуры в точках цикла. 2. Определить тепловую мощность, передаваемую воде в теплообменнике (конденсаторе). 3. Определить расход воздуха (рабочего тела). 4. Определить теоретическую потребляемую мощность. 5. Определить холодильный коэффициент. Решение: на рисунке дана принципиальная схема воздушной холодильной установки, охлаждающей помещение-1 или холодильной камеры в которой по трубам циркулирует охлажденный воздух. Конденсатор-2 всасывает этот воздух и сжимает его. 3-охладитель (конденсатор) в котором охлаждается сжатый компрессором воздух. Расширительный цилиндр -4 (детандер) в котором воздух расширяется, совершает какую-то работу, а температура понижается. Далее воздух поступает в холодильную камеру, отнимает температуру от охлаждаемых предметов (тел), сам же нагревается и снова поступает в компрессор. Цикл повторяется.
Теоретически цикл воздушно-компрессорного холодильника в PV диаграмме: т.1-характеризует состояние воздуха, поступающего в компрессор. 1-2-процесс адиабатного (изоэнтропного) сжатия в компрессоре. т.2-характеризует состояние воздуха, поступающего в расширитель. 2-3-изабарное охлаждение в конденсаторе. т.3-характеризует состояние воздуха, поступающего в расширитель. 3-4-адиабатное (изоэнтропное) расширение в детандере. 4-состояние воздуха поступающего в холодильную камеру. 4-1-процесс нагревания воздуха в этой камере. Площадь 1-2-6-5-1 измеряет работу затраченную компрессором на сжатие, а площадь3-6-5-4-3- работа, полученная в расширительном цилиндре =>затрата работы в теоретическом цикле воздушной холодильной машины измеряется площадью 1-2-3-4-1. А количество теплоты, отнятой от охлажденных тел, равняется количеству теплоты воспринятой воздухом в процессе 4-1. Площадь под линией 4-1 соответствует количеству теплоты отнятой от охлаждаемых тел. Под линией 2-3 теплота, переданная воде в охладителе. Площадь 1-2-3-4-1- соответствует работе затраченной в цикле. Данные для расчета:
1. Хладопроизводительность 1 кг воздуха: q0=i1-i4= Ср∙(T1-T4)=83 кДж/кг Т1 и Т4-температуры воздуха выходящей и поступающей в воздушно- компрессорный холодильник. Ср- изобарная теплоемкость (Ср=1.008 кДж/(кг∙К)). Температуру Т2 и Т4 найдем из соотношений адиабатного процесса: T4/T3=(P4/P3)(K-1)/K,т.к. Р3=Р2, а Р4=Р1=>Т4/T3=(P1/P2) (K-1)/K => => Т4=T3∙ (Р1/Р2) (K-1)/K =177 К Т2=T1∙ (Р2/Р1) (K-1)/K =432 К 2. Работу затраченную компрессором l найдем: l k =i2-i1= Ср∙(T2-T1)=174 кДж/кг 3. Работа в детандере: l д =i3-i4= Ср∙(T3-T4)=120 кДж/кг 4. Работа в цикле: l ц= lk - l д=54 кДж/кг 5. Расход хладагента: М= Qх/ q0=1927 кг/с 6. Холодильный коэффициент: Е= q0/ l ц=1.53 7. Nт- теоретическая мощность необходимая для привода компрессора: Nт=M∙ l ц=104 кВт Контрольный вопрос: Воздушно-компрессорная холодильная установка уступает паровой компрессорной холодильной установке по величине холодильного коэффициента и габаритам, но выигрывает у неё в меньших затратах работы за счет наличия детандера в котором часть её возвращается. Воздушно-компрессорная холодильная установка уступает абсорбционной вследствие высокой затраты работы на сжатие воздуха. К преимуществам воздушной по сравнению с абсорбционной холодильной установкой можно отнести меньшие габариты и более низкий расход охладителя для отвода теплоты от конденсатора и компрессора.
|







 кг/(кВт∙ч)
кг/(кВт∙ч)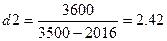 кг/(кВт∙ч)
кг/(кВт∙ч) Прямоточный
Прямоточный Противоточный
Противоточный

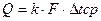 , Вт =>
, Вт => 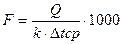 , м2, где
, м2, где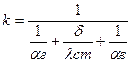 , Вт/(м2∙К)
, Вт/(м2∙К)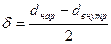 ,м
,м , где Δtб – наибольшая разность между теплоносителями; Δtм - наименьшая разность между теплоносителями.
, где Δtб – наибольшая разность между теплоносителями; Δtм - наименьшая разность между теплоносителями.

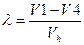 к=1.4
к=1.4
 , где lk – полная работа компрессора.
, где lk – полная работа компрессора.