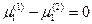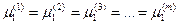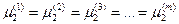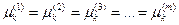Теорема равновесия Гиббса
Условие термодинамического равновесия в гетерогенной системе Пусть есть система, состоящая из К независимых компонентов и m фаз. Условимся индексировать номера компонентов арабскими цифрами внизу и номера фаз вверху соответствующих букв. Пример: через При p,T=const равновесие в такой системе наступит при минимальном значении энергии Гиббса dG=0. Энергия Гиббса будет складываться из значений этой энергии для фаз системы:
Тогда
С учетом (2) уравнение (1) перепишем в следующем виде:
Предположим теперь, что без нарушения равновесия из I-ой фазы во II-ую перешло бесконечно малое количество 1-го компонента, а числа молей этого компонента во всех других фазах и числа молей всех компонентов в остальных фазах (от 3 до К) постоянны. Тогда условие (3) перепишется в виде
В соответствии с законом сохранения массы Тогда
В отношении других компонентов во всех независимых парах фаз получим, что химический потенциал одинаков во всех фазах.
………………………
Эти соотношения выражают условие т/д равновесия в гетерогенной системе и получили название теоремы равновесия Гиббса: Условием т/д равновесия в гетерогенной системе является равенство химических потенциалов каждого из компонентов во всех фазах данной системы при постоянных р,Т или V,T.
|

 обозначим число молей i -того компонента в j -той фазе.
обозначим число молей i -того компонента в j -той фазе.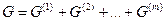
 (1)
(1) (2)
(2) (3)
(3)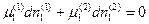

 , но согласно условию второй множитель не равен 0 (
, но согласно условию второй множитель не равен 0 ( ). Следовательно,
). Следовательно,