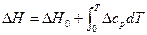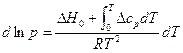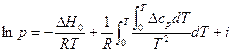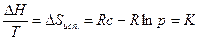Уравнение состояния однокомпонентной двухфазной системы
В соответствии с правилом фаз Гиббса при равновесии химический потенциал компонента одинаков в обеих фазах.
где μ/ - химический потенциал для одной системы μ// - химический потенциал для другой системы
Перепишем данное уравнение в следующем виде, произведя замены:
Оно позволяет рассчитать Если применить данное уравнение к процессам плавления веществ, то на основе справочных данных можно рассчитать величину Применим теперь это уравнение к процессам возгонки и испарения. Поскольку мольный объем пара значительно больше Vm жидкости или твердого тела
Если паровая фаза идеальна, то Тогда
Проинтегрируем его в узком интервале температур, считая ∆Н постоянной величиной (∆Н – теплота возгонки или испарения, зависит от температуры). Получим С помощью данного уравнения можно: 1) рассчитывать давление насыщенного пара р2 при любой температуре Т2, если известно давление р1 при какой-либо одной температуре Т1, а также известна мольная теплота парообразования. 2) рассчитывать температуру кипения жидкости Т2 при любом давлении р2, если известна температура кипения вещества Т1 при каком-либо давлении р1, а также известна мольная теплота парообразования ∆Н. 3) рассчитывать среднюю теплоту испарения или возгонки ∆Н, если известно давление насыщенного пара р по крайней мере при двух значениях температуры. 1. Проинтегрируем (4) в неопределенных пределах, учитывая зависимость ∆Н от температуры. В соответствии с уравнением Кирхгоффа:
Получим:
где i – химическая постоянная, которая является одной из важнейших характеристик вещества (табл.). 2. Проинтегрируем (4) в неопределенных пределах, пренебрегая зависимостью ∆Н от температуры. Получим:
где с – константа интегрирования. Применим уравнение к случаю испарения различных жидкостей при постоянном давлении.
При p=const правая часть уравнения - постоянная величина. В результате имеем: мольная энтропия испарения различных жидкостей при p=const есть величина постоянная (правило Трутона). К – константа Трутона, имеет размерность энтропии. Жидкости, которые подчиняются правилу Трутона, называются нормальными. Константа Трутона для таких жидкостей равна 21-22 кал/град·моль. Жидкости, молекулы которых склонны к образованию водородных связей (вода, спирт, амины и т.д.) обнаруживают отклонение от правила Трутона. Это аномальные жидкости. Для них ∆S>К.
|

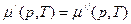
 (1)
(1)
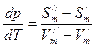 - изменение энтропии при переходе 1 моль вещества из первой фазы во вторую.
- изменение энтропии при переходе 1 моль вещества из первой фазы во вторую.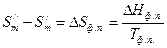
 - уравнение Клаузиуса-Клапейрона – уравнение состояния однокомпонентной системы. (2)
- уравнение Клаузиуса-Клапейрона – уравнение состояния однокомпонентной системы. (2)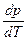 , которое показывает, на сколько надо изменить давление системы для изменения температуры фазового превращения на один градус.
, которое показывает, на сколько надо изменить давление системы для изменения температуры фазового превращения на один градус.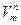 >>
>>  , то
, то 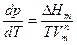 .
.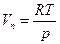
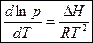 - уравнение Клаузиуса-Клапейрона для процессов возгонки испарения. (3)
- уравнение Клаузиуса-Клапейрона для процессов возгонки испарения. (3)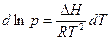 (4)
(4) (5)
(5)