НАЧАЛЬНЫЕ ПОНЯТИЯ О СЕТЯХ И ОРГРАФАХ
Ориентированный граф (орграф) § § Элементы множества Вершины орграфа i и j называются смежными, если Здесь od(k) – полустепень исхода, т.е. число дуг, начинающихся в k (исходящих из k); id(k) – полустепень захода, то есть число дуг, заканчивающихся (заходящих) в k. В дальнейшем из рассмотрения исключаются орграфы с повторяющимися (кратными) дугами и петлями – дугами, которые соединяют вершину саму с собой. Наглядным представлением орграфа является диаграмма, на которой вершины изображаются произвольно расположенными на плоскости точками. Дуги изображаются стрелками, которые соединяют между собой точки, соответствующие смежным вершинам. Следуя [1], определим путь, соединяющий в орграфе
В последовательности (1) вершины и дуги не повторяются и
Замкнутый путь, в котором
то такая последовательность будет определять полупуть, соединяющий вершины Следуя терминологии, принятой в [2], определим транспортную сеть N как связный орграф без контуров и петель, удовлетворяющий следующим условиям. § Существует только одна вершина с нулевой полустепенью захода. Эта вершина называется источником и обозначается через s. § Существует только одна вершина с нулевой полустепенью исхода. Эта вершина называется стоком и обозначается через t. § Каждой дуге
|

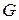 - совокупность двух конечных множеств
- совокупность двух конечных множеств  таких что:
таких что: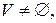 то есть множество
то есть множество  не пустое;
не пустое; , то есть множество A состоит из упорядоченных пар элементов множества
, то есть множество A состоит из упорядоченных пар элементов множества 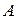 – дугами орграфа. Вершины орграфа будем в дальнейшем обозначать их порядковыми номерами, дуги – упорядоченными парами номеров вершин.
– дугами орграфа. Вершины орграфа будем в дальнейшем обозначать их порядковыми номерами, дуги – упорядоченными парами номеров вершин.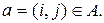 Дуга
Дуга  в этом случае называется инцидентной вершинам i и j. Число дуг, инцидентных данной вершине k, называется степенью вершины и обозначается
в этом случае называется инцидентной вершинам i и j. Число дуг, инцидентных данной вершине k, называется степенью вершины и обозначается 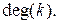 Степень вершины в орграфе можно представить в виде deg(k) = od(k)+ id(k).
Степень вершины в орграфе можно представить в виде deg(k) = od(k)+ id(k). и
и  как последовательность чередующихся вершин и дуг:
как последовательность чередующихся вершин и дуг: (1)
(1)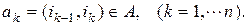
 называется контуром. Если допустить, что в последовательности вида (1)
называется контуром. Если допустить, что в последовательности вида (1)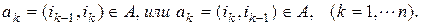
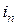 . Вершину
. Вершину  в сети
в сети 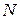 сопоставлено неотрицательное вещественное число
сопоставлено неотрицательное вещественное число 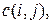 называемое пропускной способностью дуги; если дуги
называемое пропускной способностью дуги; если дуги 



