Построение изображений в линзах
ГРАФИЧЕСКАЯ РАБОТА № 1 Построение изображений предметов в линзах
Цель работы: изучить способы построения изображений предметов в линзах.
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
Линзы
Лучи, идущие параллельно главной оптической оси, отклоняются за собирающей линзой (а) так, что собираются в точке, называемой фокусом. В рассеивающей линзе лучи, идущие параллельно главной оптической оси, отклоняются так, что в фокусе, находящемся со стороны падающих лучей, собираются их продолжения (б). Расстояние до фокусов с одной и другой стороны тонкой линзы одинаково и не зависит от профиля правой и левой поверхностей линзы.
Фокусное расстояние F – расстояние от центра линзы до фокуса – зависит только от показателя преломления n материала линзы и радиусов кривизны сфер, ограничивающих поверхность линзы: например, для двояковыпуклой собирающей линзы, ограниченной сферами с радиусами R 1 и R 2,
Расстояние d от точечного источника до линзы связано с расстоянием f от линзы до его изображения и фокусным расстоянием F линзы соотношением
Это соотношение и называют формулой тонкой линзы. Знак «+» перед Величина
Отношение размера изображения Н в направлении, перпендикулярном главной оптической оси, к размеру предмета h в этом направлении называется линейным увеличением предмета в тонкой линзе (обозначается буквой Г). Для тонкой линзы можно доказать, что при любом типе изображения линейное увеличение равно:
Построение изображений в линзах
Для построения изображения в линзе любой точки объекта, достаточно найти точку пересечения каких-либо двух лучей, исходящих из этой точки. Наиболее простое построение выполняется при помощи лучей, указанных на рисунке.
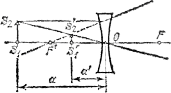
Луч 3 проходит через передний фокус F; преломляясь, этот луч идет параллельно главной оптической оси. Построение этих лучей выполняется без всяких затруднений. Всякий другой луч, идущий из точки S2, построить выло бы значительно труднее — пришлось бы непосредственно использовать закон преломления. Но в этом и нет необходимости, так как после выполнения построения любой преломленный луч пройдет через точку S2'.
Следует отметить, что при решении задачи о построении изображения внеосевых точек вовсе не необходимо, чтобы выбранные простейшие пары лучей действительно проходили через линзу (или зеркало). Во многих случаях, например при фотографировании, предмет значительно больше линзы, и лучи 2 и 3 не проходят через линзу. Тем не менее эти лучи могут быть использованы для построения изображения. Peaльные лучи, участвующие в образовании изображения, ограничены оправой линзы (заштрихованные конусы), но с ходя т с я, конечно, в той же точке S'2, поскольку доказано, что при преломлении в линзе изображением точечного источника является снова точка.
1. Предмет находится от линзы на расстоянии, большем двойного фокусного расстояния. Таково обычно положение предмета при фотографировании. Построение изображения дано на рисунке. Поскольку a>2f, то изображение лежит между задним фокусом и точкой, находящейся на двойном фокусном расстоянии от оптического центра линзы. Изображение — перевернутое (обратное) и уменьшенное.
2. Отметим важный частный случай, когда на линзу падает пучок лучей, параллельных какой-либо побочной оптической оси. Подобный случай имеет место, например, при фотографировании очень удаленных протяженных предметов. В этом случае изображение лежит на соответствующей побочной оптической оси, в месте ее пересечения с задней фокальной плоскостью (так называется плоскость, перпендикулярная к главной оси и проходящая через задний фокус линзы) Точки фокальной плоскости нередко называют фокусами соответствующих побочных осей, оставляя название главный фокус за точкой F', соответствующей главной оси.
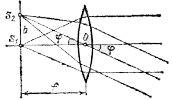
3. Предмет лежит между точкой на двойном фокусном расстоянии и передним фокусом — обычное положение предмета при проецировании проекционным фонарем. Для исследования этого случая достаточно воспользоваться свойством обратимости изображения в линзе. Будем считать S'1S'2 источником тогда S1S2 будет являться изображением. Легко видеть, что в рассматриваемом случае изображение — обратное, увеличенное и лежит от линзы на расстоянии, большем двойного фокусного расстояния. Полезно отметить частный случай, когда предмет находится от линзы на расстоянии, равном двойному фокусному расстоянию. Тогда изображение лежит от линзы также на двойном фокусном расстоянии. Изображение в этом случае перевернутое, имеет те же размеры, что и предмет.
4. Большое значение имеет частный случай, когда источник находится в плоскости, перпендикулярной к главной оси линзы и проходящей через передний фокус. Эта. плоскость также является фокальной плоскостью; ее называют передней фокальной плоскостью. Если точечный источник находится в какой-либо из точек фокальной плоскости, т. е. в одном из передних фокусов, то из линзы выходит параллельный пучок лучей, направленный вдоль соответствующей оптической оси.
5. Предмет лежит между передним фокусом и линзой. В этом случае изображение—прямое, мнимое, увеличенное. Построение изображения в этом случае дано на рисунке. т. е. изображение увеличенное. Этот случай соответствует лупы.
6. Построение изображения для рассеивающей линзы
Отметим, что при всех построениях лучей, проходящих через тонкую линзу, мы можем не рассматривать ход их внутри самой линзы. Важно лишь знать расположение оптического центра и главных фокусов. Таким образом, тонкая линза может быть изображена плоскостью, проходящей через оптический центр перпендикулярно к главной оптической оси, на которой должны быть отмечены положения главных фокусов. Эта плоскость называется главной плоскостью. Очевидно, что луч, входящий в линзу и выходящий из нее, проходит через одну и ту же точку главной плоскости. Если мы сохраняем на рисунках очертания линзы, то только для
|

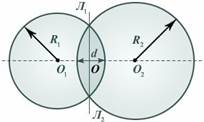 Сферическая линза представляет собой однородное прозрачное тело, ограниченное двумя сферическими поверхностями. Линия О 1 О 2, соединяющая центры сфер, ограничивающие поверхность линзы, называется главной оптической осью линзы. Плоскость Л 1 Л 2, проходящая через линию пересечения сфер, ограничивающих линзу, называется плоскостью линзы. Плоскость линзы перпендикулярна главной оптической оси линзы. Точка О пересечения плоскости линзы и ее главной оптической оси называется центром линзы. Отрезок оптической оси, заключенный между сферами, ограничивающими линзу, называется толщиной линзы d. Линза называется тонкой, если d << R 1 и d << R 2, где R 1 и R 2 – радиусы сфер, ограничивающих линзу. Эти радиусы называются радиусами кривизны поверхностей линзы.
Сферическая линза представляет собой однородное прозрачное тело, ограниченное двумя сферическими поверхностями. Линия О 1 О 2, соединяющая центры сфер, ограничивающие поверхность линзы, называется главной оптической осью линзы. Плоскость Л 1 Л 2, проходящая через линию пересечения сфер, ограничивающих линзу, называется плоскостью линзы. Плоскость линзы перпендикулярна главной оптической оси линзы. Точка О пересечения плоскости линзы и ее главной оптической оси называется центром линзы. Отрезок оптической оси, заключенный между сферами, ограничивающими линзу, называется толщиной линзы d. Линза называется тонкой, если d << R 1 и d << R 2, где R 1 и R 2 – радиусы сфер, ограничивающих линзу. Эти радиусы называются радиусами кривизны поверхностей линзы.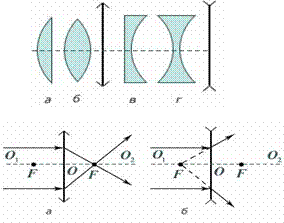 На рисунке представлены простейшие профили стеклянных линз: плоско-выпуклая (а), двояковыпуклая (б), плоско-вогнутая (в), и двояковогнутая (г). Первые две из них в воздухе являются собирающими линзами, а вторые две – рассеивающими. Эти названия связаны с тем, что в собирающей линзе луч, преломляясь, отклоняется в сторону оптической оси, а в рассеивающей наоборот.
На рисунке представлены простейшие профили стеклянных линз: плоско-выпуклая (а), двояковыпуклая (б), плоско-вогнутая (в), и двояковогнутая (г). Первые две из них в воздухе являются собирающими линзами, а вторые две – рассеивающими. Эти названия связаны с тем, что в собирающей линзе луч, преломляясь, отклоняется в сторону оптической оси, а в рассеивающей наоборот.
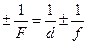
 ставится в случае действительного изображения, знак «–» - в случае мнимого изображения.
ставится в случае действительного изображения, знак «–» - в случае мнимого изображения.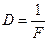 называется оптической силой линзы. Если фокусное расстояние F выражено в метрах, то оптическая сила линзы D получается в диоптриях (дптр). Оптическая сила собирающей линзы считается положительной, рассеивающей линзы – отрицательной.
называется оптической силой линзы. Если фокусное расстояние F выражено в метрах, то оптическая сила линзы D получается в диоптриях (дптр). Оптическая сила собирающей линзы считается положительной, рассеивающей линзы – отрицательной. .
.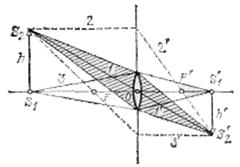 Луч 1 идет вдоль побочной оптической оси без изменения направления. Луч 2 падает на линзу параллельно главной оптической оси; преломляясь, этот луч проходит через задний фокус F'.
Луч 1 идет вдоль побочной оптической оси без изменения направления. Луч 2 падает на линзу параллельно главной оптической оси; преломляясь, этот луч проходит через задний фокус F'. Рассмотрим несколько типичных случаев изображения в линзе. Линзу будем считать собирающей.
Рассмотрим несколько типичных случаев изображения в линзе. Линзу будем считать собирающей.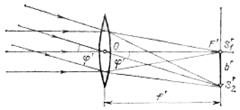
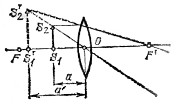
 Изображение в рассеивающей линзе всегда мнимое и прямое.
Изображение в рассеивающей линзе всегда мнимое и прямое.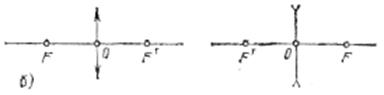 наглядного различия собирающей и рассеивающей линз; для всех же построений эти очертания излишни. Иногда для большей простоты чертежа вместо очертаний линзы применяют символическое изображение.
наглядного различия собирающей и рассеивающей линз; для всех же построений эти очертания излишни. Иногда для большей простоты чертежа вместо очертаний линзы применяют символическое изображение.


