Метод парабол (метод Симпсона)
Использовав три точки отрезка интегрирования, можно заменить подынтегральную функцию параболой. Обычно в качестве таких точек используют концы отрезка и его среднюю точку. В этом случае формула имеет очень простой вид
Если разбить интервал интегрирования на
где 2. 1316 , получится 2 тетрады переводим 116=00012 и 316=00112, убираем незначащие 0, получаем Ответ: 100112 0,11012 ; имеется 1 тетрада 1101, переводим по табл., получаем Ответ: 0,D16
БИЛЕТ.
2. первое0,847*2=1,694(1) | 0,694*2=1,388(1) | 0,488*2=0,776(0) | 0,776*2=1,552(1) |=>; 0,84710=0,11012 Второе 0,00101012 допишем не значащий 0, получим 0,001010102 , в итоге получилось 2 тетрады 0010 и 1010 00102=216 10102=А16 Ответ: 0,2А16 БИЛЕТ. 1. Алгоритм - это последовательность инструкций для выполнения какого либо задания. Свойства алгоритма: ДИСКРЕТНОСТЬ – разделение выполнения решения задачи на отдельные операции ОПРЕДЕЛЕННОСТЬ (точность) алгоритма – определение однозначных действий исполнителя ПОНЯТНОСТЬ – не должен быть рассчитан на принятие каких-либо самостоятельных решений РЕЗУЛЬТАТИВНОСТЬ (конечность) алгоритма – исполнение алгоритма должно закончиться за конечное число шагов ФОРМЫ ЗАПИСИ АЛГОРИТМОВ v ЗАПИСАН НА ЕСТЕСТВЕННОМ ЯЗЫКЕ; v ИЗОБРАЖЕН В ВИДЕ БЛОК СХЕМЫ; v ЗАПИСАН НА АЛГОРИТМИЧЕСКОМ ЯЗЫКЕ. Анализ скорости выполнения алгоритмов Производительность алгоритма можно оценить по порядку величины. Алгоритм имеет сложность порядка O(f(N)) (произносится «О большое от F от N»), если с увеличением размерности исходных данных N время выполнения алгоритма растет пропорционально функции f(N). Сложность рекурсивных алгоритмов Рекурсивными процедурами (recursive procedure) называются процедуры, вызывающие сами себя 2. первое 0,847*16=13,552(D) 0,552*16=8,832(8) 0,832*16=13,312(D) 0,D8D Второе 0,00101012 допишем не значащий 0, получим 0,001010102 , в итоге получилось 2 тетрады 0010 и 1010 00102=216 10102=А16 Ответ: 0,2А16 БИЛЕТ. 1. Жизненный цикл программного обеспечения (ПО) — период времени, который начинается с момента принятия решения о необходимости создания программного продукта и заканчивается в момент его полного изъятия из эксплуатации.
|

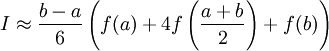 .
.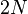 равных частей, то имеем
равных частей, то имеем
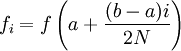 .
. 1. Метод Ньютона. Задан отрезок [а,Ь], содержащий корень уравнения F(x)=0. Уточнение значения корня производится путем использования уравнения касательной. В качестве начального приближения задается тот из концов отрезка [а,Ь], где значение функции и ее второй производной имеют одинаковые знаки (т.е. выполняется условие F(X0)*F"(X0)>0). В точке F(х0) строится касательная к кривой у= F(х) и ищется ее пересечение с осью х. Точка пересечения принимается за новую итерацию. Итерационная формула имеет вид:
1. Метод Ньютона. Задан отрезок [а,Ь], содержащий корень уравнения F(x)=0. Уточнение значения корня производится путем использования уравнения касательной. В качестве начального приближения задается тот из концов отрезка [а,Ь], где значение функции и ее второй производной имеют одинаковые знаки (т.е. выполняется условие F(X0)*F"(X0)>0). В точке F(х0) строится касательная к кривой у= F(х) и ищется ее пересечение с осью х. Точка пересечения принимается за новую итерацию. Итерационная формула имеет вид:



