Решение. Конечно же, для нахождения асимптот здесь мы не будем использовать выведенные ранее формулы, и, тем более
1) а) Конечно же, для нахождения асимптот здесь мы не будем использовать выведенные ранее формулы, и, тем более, приводить к общему знаменателю. По определению наклонной асимптоты асимптота (т.к.
что Ответ.
б)
асимптоты бесполезно.
Ответ. в)
асимптота, т.к.
Ответ. г)
вертикальная асимптота.
делаем вывод: наклонных асимптот нет. Ответ.
д)
Найдем наклонные асимптоты.
Приведем одно неверное рассуждение, подсказанное «здравым смыслом»:
Ответ. 2) Оформим (возможный) порядок выполнения этого задания: 1. Находим область определения функции. 2. Расставляем знаки функции на числовой прямой. 3. Находим асимптоты. 4. Отмечаем корни функции на координатной плоскости(или точки пересечения с осями). 5. Рисуем «хвостики» графика при подходе к вертикальным асимптотам. («Хвостик» вверху или внизу? Смотрим по картинке со знаками функции.) 6. Учитывая все уже изображенное к этому моменту, заканчиваем чертеж. Замечание. Конечно, проведенные исследования (без применения производной) дают возможность построить только очень приблизительный вариант эскиза графика!
 а) а) 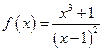 . 1. . 1. 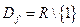 ; ;
3.
 . 1. . 1. 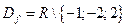 ; ;
3.
в) 2. 3.

г) 2. 3.
Для построения эскиза графика здесь необходимо знать поведение функции в окрестности 0 (тип точки разрыва):
д) 2. 3. См. выше:
е) 1. 2. 3. Предварительно вычислим пределы показателя в точках разрыва и на бесконечности, а затем воспользуемся теоремой о пределе композиции функций. Знаки показателя
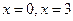 - правосторонние вертикальные асимптоты; - правосторонние вертикальные асимптоты; 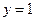 - (двусторонняя) горизонтальная асимптота. - (двусторонняя) горизонтальная асимптота.
Задания для самостоятельного решения.
1) Может ли график функции пересекать свою: а) вертикальную; б) горизонтальную; наклонную асимптоту? 2) Может ли график функции иметь: а) 2 вертикальные и 3 горизонтальные асимптоты? б) 3 вертикальные и 2 горизонтальные асимптоты? в) 1 наклонную и 5 вертикальных асимптот? г) 2 горизонтальные и 1 наклонную асимптоту? д) ровно 315 асимптот? е) бесконечно много асимптот? 3) Верно ли, что рациональная функция имеет наклонную асимптоту тогда и только тогда, когда степень числителя на 1 больше степени знаменателя? 4) Верно ли, что рациональная функция не может иметь более 1 наклонной (горизонтальной) асимптоты? 5) Приведите пример формулы, задающей функцию, график которой имеет две различные горизонтальные или наклонные асимптоты. 6) Приведите пример формулы, задающей функцию, график которой имеет любую одностороннюю асимптоту. 7) Приведите пример функции, у которой есть асимптота: а) 8) Приведите пример функции, полный набор прямолинейных асимптот которой состоит из прямых: а) в)
1) а) д)
2) Найдите область определения, промежутки знакопостоянства и полный набор асимптот, постройте эскиз графика функции: а) з) м)
3) Является ли функция
Ответы к заданиям для самостоятельного решения.
1) Нет; да; да. 2) а) Нет. б) Да. в) Да. г) Нет. д) Да. е) Да. 3) Да. 4) Да. 5) Например, 6) Например, 7) Например: а) 8) Например: а) в)
г) з) вертикальная асимптота; 2)
   а) а)
  б) б)
 Ас.: Ас.: 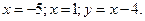
   г) г)
  д) д)
     е) е)
ж) левосторонняя наклонная
 и) и)
Ас.: вертикальная
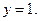
Ас.:
    л) л)
Ас.:
м)
Полностью изобразить график невозможно, т.к. кривая асциллирует,
 т.е. график «гуляет в коридоре т.е. график «гуляет в коридоре
меняя направление при приближении к 0.
н) Асимптот нет.
о)
3)
|

 .
.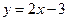 - (двусторонняя) наклонная
- (двусторонняя) наклонная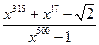 - б.м. при
- б.м. при  );
);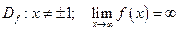 . На
. На 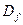 функция непрерывна как рациональная, так
функция непрерывна как рациональная, так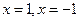 - все вертикальные асимптоты.
- все вертикальные асимптоты.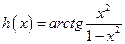 .
.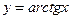 - ограниченная функция, следовательно, искать вертикальные
- ограниченная функция, следовательно, искать вертикальные .
.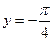 - (двусторонняя) горизонтальная асимптота.
- (двусторонняя) горизонтальная асимптота. .
.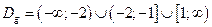 ;
; 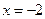 - (двусторонняя) вертикальная
- (двусторонняя) вертикальная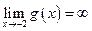 .
.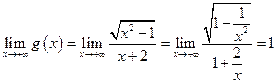 ;
; 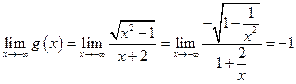 .
. - левосторонняя горизонтальная асимптота.
- левосторонняя горизонтальная асимптота.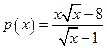 .
.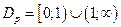 .
. 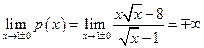 ;
; 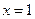 - (двусторонняя)
- (двусторонняя)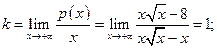
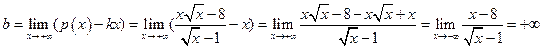 ;
;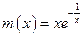 .
. .
. 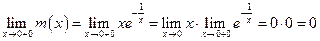 .
.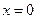 - левосторонняя вертикальная асимптота.
- левосторонняя вертикальная асимптота. 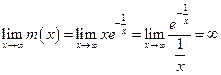 . Горизонтальных асимптот нет.
. Горизонтальных асимптот нет.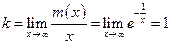 .
.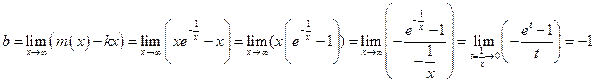 .
.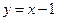 - (двусторонняя) наклонная асимптота.
- (двусторонняя) наклонная асимптота. (Казалось бы), у графика
(Казалось бы), у графика 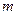 должна быть асимптота
должна быть асимптота 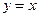 , т.к. при
, т.к. при 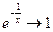 , т.е.
, т.е. 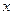 .
.


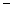
 2.
2.
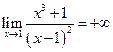 .
.

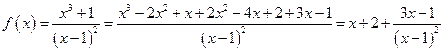 ;
; 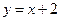 - наклонная асимптота.
- наклонная асимптота.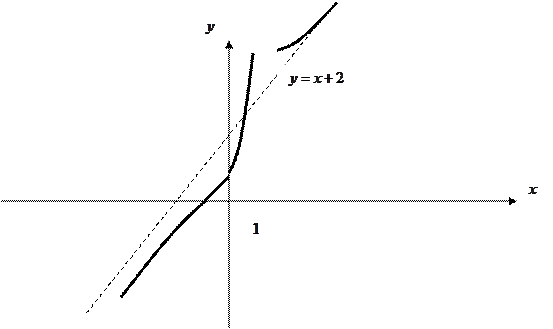



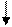

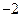
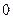
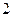
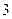
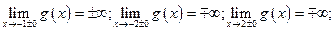
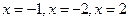 - вертикальные асимптоты.
- вертикальные асимптоты.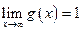 ;
; 
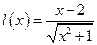 . 1.
. 1. 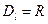 .
.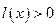 при
при 
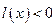 при
при 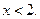
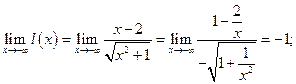
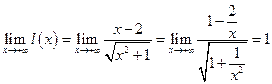 .
.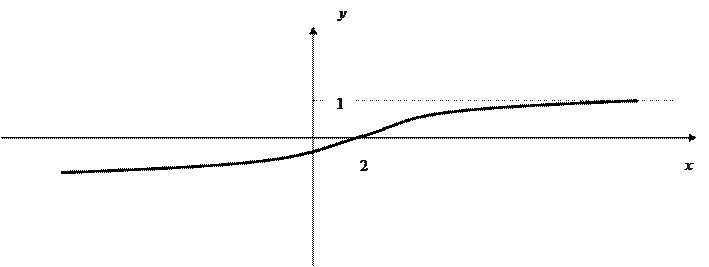
 . 1.
. 1. 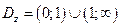 .
.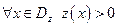 .
.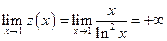 ;
; 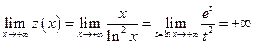 ; горизонтальных асимптот нет.
; горизонтальных асимптот нет.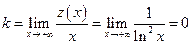 ; наклонных асимптот нет (
; наклонных асимптот нет ( , наклонная асимптота «вырождается» в горизонтальную, а горизонтальных асимптот нет).
, наклонная асимптота «вырождается» в горизонтальную, а горизонтальных асимптот нет).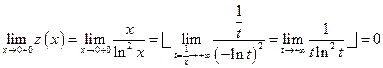 (выделенная часть вычислений необязательна: и ранее видно, что предел имеет вид
(выделенная часть вычислений необязательна: и ранее видно, что предел имеет вид 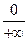 ).
).
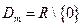 .
.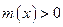 при
при 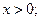
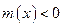 при
при 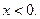
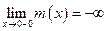 .
. 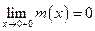 .
. 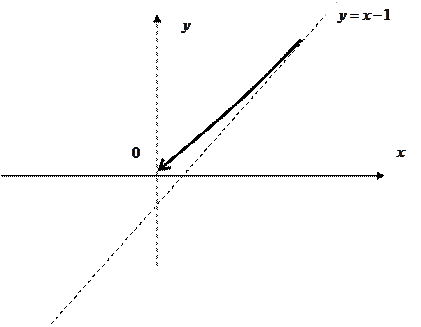

 .
. .
.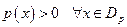 .
.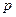 непрерывна на
непрерывна на 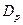 . Точки разрыва:
. Точки разрыва: 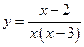 :
:
 ;
;  ;
; 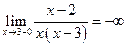 ;
; 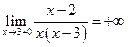 ;
;  .
.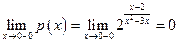 ;
; 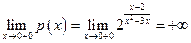 ;
; 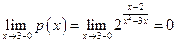 ;
;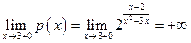 ;
; 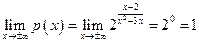 .
.
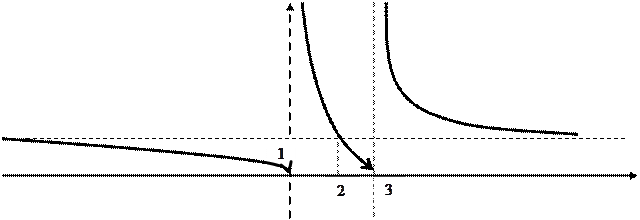

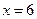 ; б)
; б) 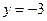 ; в)
; в) 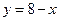 .
.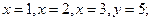 б)
б) 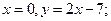
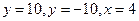 ; г)
; г) 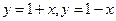 .
. Найдите полный набор асимптот графика функции:
Найдите полный набор асимптот графика функции: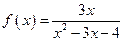 ; б)
; б) 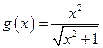 ; в)
; в) 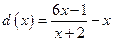 ; г)
; г) 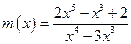 ;
;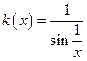 ; е)
; е) 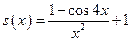 ; ж) (в)
; ж) (в) 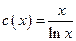 ; з) (в)
; з) (в) 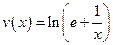 .
.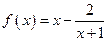 ; б)
; б) 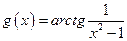 ; в)
; в) 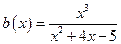 ; г)
; г) 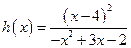 ; д)
; д) 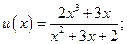 е)
е) 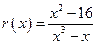 ; ж)
; ж) 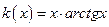 ;
;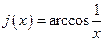 ; и)
; и) 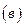
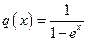 ; к)
; к) 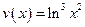 ; л)
; л) 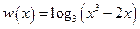 ;
;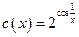 ; н)
; н) 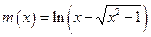 ; о)
; о) 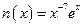 .
.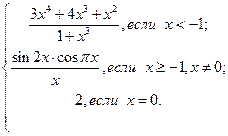 непрерывной на R? Есть ли у ее графика асимптоты? Ответ обоснуйте.
непрерывной на R? Есть ли у ее графика асимптоты? Ответ обоснуйте.
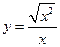 , или
, или 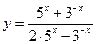 ,...
,...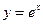 , или
, или 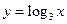 ,...
,...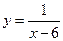 ,... б)
,... б) 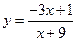 ,... в)
,... в) 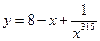 ,...
,...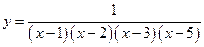 ,... б)
,... б) 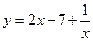 ,...
,...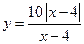 ,... г)
,... г) 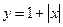 ,...
,...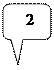 1) а)
1) а) 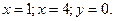 б)
б) 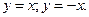 в)
в) 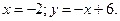
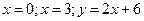 . д)
. д) 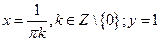 . е)
. е) 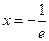 - левосторонняя
- левосторонняя



 Ас.:
Ас.: 
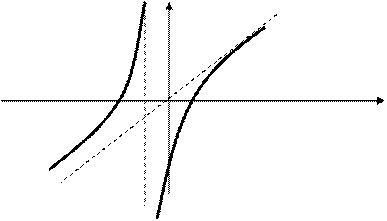


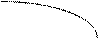
 Ас.:
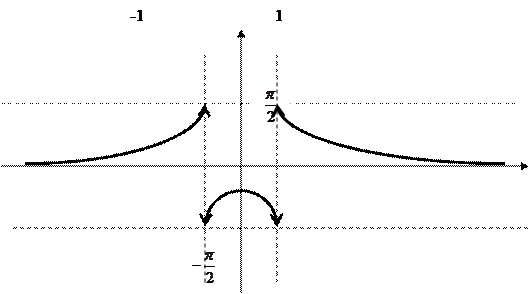
Ас.: 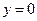 .
.
 в)
в)
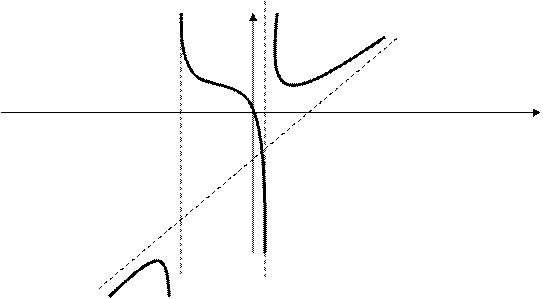



 Ас.:
Ас.: 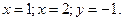



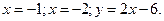
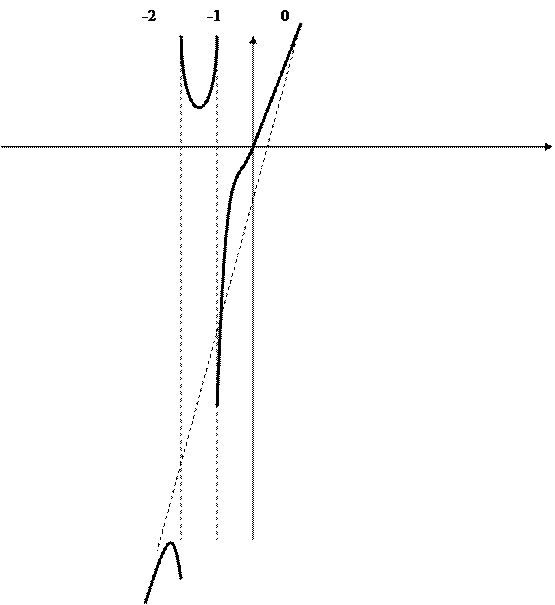






 Ас.:
Ас.: 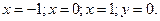
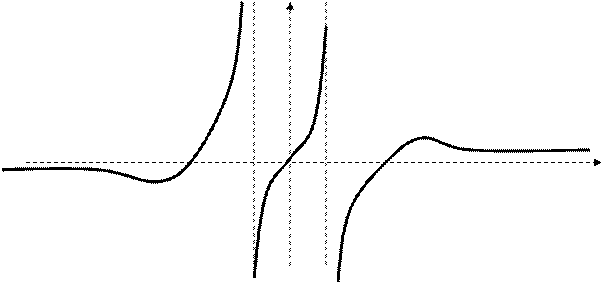
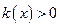 при
при 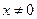 ; асимптоты: правосторонняя наклонная
; асимптоты: правосторонняя наклонная 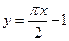 ;
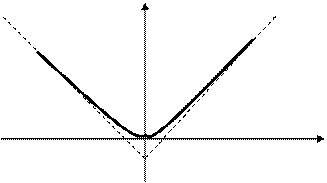
;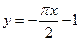 .
.
 з)
з) 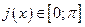 ;
; 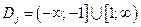 . Ас.:
. Ас.: 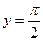 .
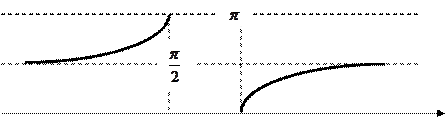
. 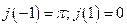 .
.
 правосторонняя горизонтальная
правосторонняя горизонтальная 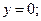
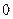
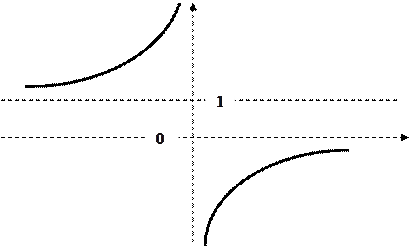
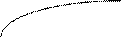
 к)
к)
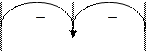

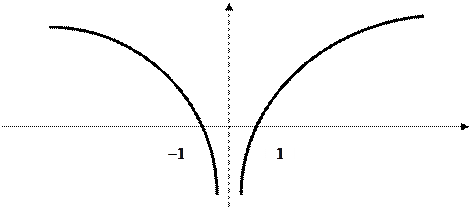




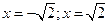 - правосторонние вертикальные;
- правосторонние вертикальные; 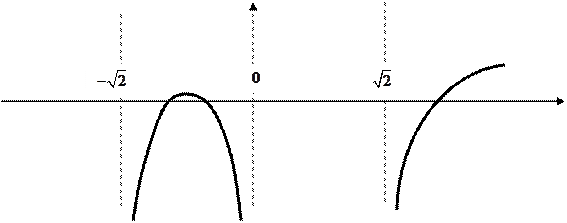
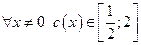 ;
; 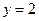 - горизонтальная асимптота.
- горизонтальная асимптота.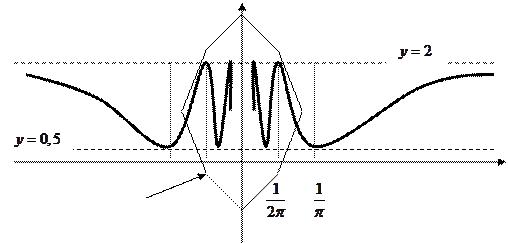

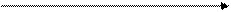 между
между 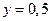 и
и 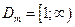 ;
; 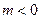 при
при 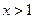 ;
; 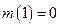 .
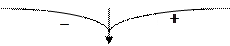
.

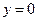 - левосторонняя горизонтальная асимптота.
- левосторонняя горизонтальная асимптота.
 непрерывна на
непрерывна на 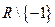 ;
; 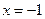 - точка разрыва 1-го рода.
- точка разрыва 1-го рода.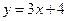 - левосторонняя наклонная асимптота;
- левосторонняя наклонная асимптота; 


