Асимптоты графика функции.
I. Определение. Прямая
Если только называется соответственно левосторонней или правосторонней вертикальной асимптотой.
вертикальная асимптота.
б)
асимптоты.
(в) в)
вертикальная асимптота.
Кривая т.е. Пример. Далее мы будем рассматривать только прямолинейные асимптоты.
II. Горизонтальные асимптоты возникают в том случае, если на бесконечностифункция имеет конечный предел.
Определение. Прямая
Если только называется соответственно левосторонней или правосторонней горизонтальной асимптотой. Примеры. а)
б)
(в) в)
III. Наклонные асимптоты. Определение. Прямая
Если только прямая наклонной асимптотой. Способы отыскания наклонных асимптот: 1) По определению. Если
Замечание. Этот способ дает возможность по знаку остатка определить, проходит график функции выше или ниже асимптоты. Вообще, если
2) Выведем формулы для нахождения
 , здесь , здесь  и и  - б.м. при - б.м. при 
Пример.
Горизонтальная асимптота – частный случай наклонной (при
Задание. 1) Найти полный набор асимптот графика функции: а) (в) д) 2)Найти область определения, промежутки знакопостоянства и полный набор асимптот, построить эскиз графика функции: а)
|

 Вертикальные асимптоты возникают в том случае, если в конечной точке функция имеет бесконечный предел.
Вертикальные асимптоты возникают в том случае, если в конечной точке функция имеет бесконечный предел.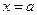 называется вертикальной асимптотой графика функции
называется вертикальной асимптотой графика функции , если
, если  .
.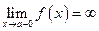 или
или 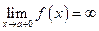 , то прямая
, то прямая 

 Примеры. а)
Примеры. а) 
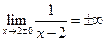


 - (двусторонняя)
- (двусторонняя)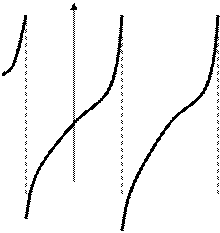

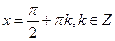 -
-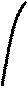
 (двусторонние) вертикальные
(двусторонние) вертикальные
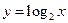


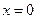 - правосторонняя
- правосторонняя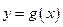 называется асимптотой графика функции
называется асимптотой графика функции 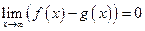 ,
,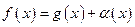 , где
, где 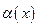 - б.м. при
- б.м. при 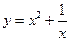 . Криволинейная асимптота -
. Криволинейная асимптота -  . Т.о. на бесконечности график функции приближается к параболе
. Т.о. на бесконечности график функции приближается к параболе  называется горизонтальной асимптотой графика функции
называется горизонтальной асимптотой графика функции .
.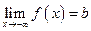 или
или  , то прямая
, то прямая 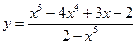
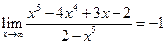 .
. - (двусторонняя) горизонтальная асимптота.
- (двусторонняя) горизонтальная асимптота.

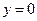 - (двусторонняя) горизонтальная асимптота.
- (двусторонняя) горизонтальная асимптота.

 называется наклонной асимптотой графика функции
называется наклонной асимптотой графика функции .
.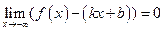 или
или  , то
, то , где
, где  , то можно разделить
, то можно разделить  на
на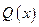 «уголком».
«уголком».
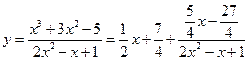
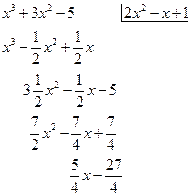
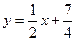 - (двусторонняя) наклонная асимптота.
- (двусторонняя) наклонная асимптота.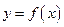 , то по знаку разности
, то по знаку разности 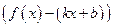 можно определить расположение графика относительно асимптоты на том или ином промежутке.
можно определить расположение графика относительно асимптоты на том или ином промежутке. и
и 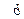 в уравнении наклонной асимптоты.
в уравнении наклонной асимптоты.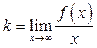
 , т.е.
, т.е.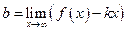
 , т.е.
, т.е. .
.
 .
.
 ).
).
 ; б)
; б) 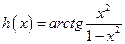 ; в)
; в)  ; г)
; г) 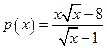 ;
;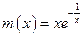 .
.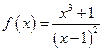 ; б)
; б)  ; в)
; в) 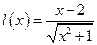 ; (в) г)
; (в) г)  ; (в) д)
; (в) д)  .
.


