Проектный расчет. Расчет геометрии колес передачи
Ориентировочное значение межосевого расстояния aw определяют по условию контактной выносливости зубьев колеса согласно расчетным зависимостям [5, с. 153]:
где Т1H – расчетный крутящий момент на ведущем валу передачи, Н.м; s HР2 – допускаемые контактные напряжения для зубьев колеса, МПа, К1 – расчетный коэффициент; для прямозубых колес К1 = 450, для косозубых и шевронных колес К1 = 410 [1, с.18]. Рассчитанное значение межосевого расстояния aw необходимо согласовать со стандартным рядом (табл. 5.1), если проектируют стандартный редуктор.
Таблица 5.1 – Межосевое расстояние зубчатых передач по ГОСТ 2185-66
Примечание. Первый ряд предпочтительнее второму.
При проектировании нестандартного редуктора следует использовать значение межосевого расстояния,округленное до ближайшего большего числа из нормальных линейных рядов по ГОСТ 6636-69. Диапазон величин нормального модуля mn: mn = (0,01 …0,02) ·aw Нормальный модуль передачи mn согласуют со стандартным значением (табл. 5.2), входящим в рассчитанный диапазон.
Таблица 5.2 - Модули зубчатых передач по ГОСТ 9563-60
Примечание. Первый ряд предпочтительнее второму.
Зависимости для расчета суммарного числа зубьев в передаче Z Σ, числа зубьев шестерни Z 1 и колеса Z 2 приведены в табл. 5.3. Для расчета чисел зубьев косозубой передачи предварительно можно принять угол наклона зубьев β; = 100 . Для раздвоенной шевронной передачи и шевронной передачи значение угла β; выбирают из диапазона: 250… 400.
Таблица 5.3 – Зависимости для расчета чисел зубьев в цилиндрической передаче
Примечание. Рассчитанные числа зубьевнеобходимо округлить до целого числа.
По округленным значениям чисел зубьев шестерни Z 1 и колеса Z 2 уточняют фактическое передаточное число u факт и его отклонение от стандартного значения ∆ u: uфакт = Z 2 / Z 1 Затем уточняют величину угла наклона зубьев колес b:
Вычисление cos b надо выполнять с точностью до пяти цифр после запятой. Делительные диаметры шестерни d 1 и колеса d 2:
В (5.2) для прямозубой передачи cos β = 1.
Правильность выполненных расчетов проверяют по зависимости:
Если межосевое расстояние, вычисленное по (5.3), получилось равным стандартному значению без округления, то это означает, что делительные диаметры рассчитаны правильно, и можно продолжать расчет геометрических параметров шестерни и колеса. В противном случае необходимо уточнить величину «cos β» и повторить расчеты по (5.2) и ф.(5.3). Диаметры окружностей вершин зубьев шестерни и колеса: da1 = d1 + 2 . mn, da2 = d2 + 2 . mn Диаметры окружностей впадин зубьев шестерни и колеса: df 1 = d1 – 2,5 . mn, df 2= d2 – 2,5 . mn
Ширина зубчатого венца колеса: bW2 = Ψ ba · a w (5.4) При расчете раздвоенной шевронной передачи следует помнить, что крутящий момент с одного вала на другой передается с помощью двух пар колес. Следовательно, рассчитанная по (5.4) величина bW2 – это ширина зубчатых венцов двух колес. При монтаже передачи возможен относительный осевой сдвиг зубьев шестерни и колеса. Чтобы гарантированно обеспечить длину контактной поверхности зубьев, заложенную в расчеты, необходимо изготовить шестерню большей ширины, чем колесо: bW1 = bW 2 + (3…5) мм Рассчитанные величины bW1 и bW 2 необходимо округлить до ближайшего значения по нормальным линейным размерам согласно ГОСТ 6636-69
|
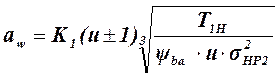, мм (1)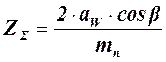
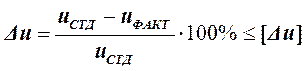
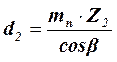(5.2)
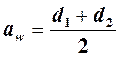(5.3)
