нескінченного періодичного десяткового дробу
Множина всіх дробів, що позначають одну і ту ж саму величину утворюють клас еквівалентних дробів. Такий клас еквівалентних дробів називають раціональним числом. Для вивчення властивостей такого раціонального числа розглядають представника цього класу, тобто дріб Будь-яке раціональне число може бути представлене у вигляді десяткового дробу. Якщо у розкладі знаменника n раціонального числа на прості множники присутні тільки прості множники 2 і 5, то цей десятковий дріб є скінченим; якщо ж у цьому розкладі є інші прості множники, то десятковий дріб буде нескінченним. Наприклад, Нескінчений десятковий дріб називається періодичним, якщо, починаючи з якогось місця у ньому повторюється одна чи декілька цифр. Наприклад, у дробі 0,1666…, починаючи з другого місці від коми (з сотих), повторюється цифра 6. У дробі 0,2626… зразу після коми повторюється група цифр 26. Така група цифр, яка послідовно повторюється після коми у десятковому записі числа, називається періодом. Період прийнято записувати один раз у круглих дужках.0,16666… = 0,1(6). 5,2626…=5,(26). Розрізняють чисті періодичні дроби – в них період починається зразу після коми, і мішані періодичні дроби – в них між комою і періодом є інші цифри. 0,(32) – чистий періодичний дріб, 0, 37(3) – мішаний періодичний десятковий дріб. Будь-який скінчений десятковий дріб можна зробити нескінченим періодичним, приписавши справа довільну кількість нулів, тобто скінчений десятковий дріб можна вважати нескінченим періодичним дробом з періодом, що складається із цифри 0. Раціональне число – це нескінченний періодичний десятковий дріб. Щоб записати додатне раціональне число а)
Завдання 5. Запишіть у вигляді звичайних дробі такі нескінчені періодичні десяткові дроби: а) 0,(3); б) 0,23(7).
2.3. Проценти Дроби із сталим знаменником 100 називають процентами. Процент – це одна сота частина числа або одиниці. Позначається знаком %. Використовується для позначення частки чого-небудь о відношенню до цілого. Наприклад, 17% від 500кг означає 17 частин по Розрізняють три основних види задач на проценти. Перша задача (пряма) – знаходження процентів від числа: У школі 800 учнів. 30% - учні молодших класів. Скільки у школі учнів молодших класів?
Перша обернена їй задача – знаходження числа за його процентом: У школі 240 учнів початкових класів, що становить 30% від усіх учнів школи. Скільки всього учнів у школі?
Друга обернена їй задача – знаходження процентного відношення двох чисел: У школі 800 учнів, з них 240 – учні початкових класів. Скільки процентів становлять учні молодших класів від числа всіх учнів школи?
Завдання 6: Вирахуйте процент успішності і процент якості знань у групі студентів, якщо у цій групі 28 студентів, 26 студентів мають задовільні оцінки, один студент має дві незадовільних оцінки, другий студент має одну незадовільну оцінку, у групі 3 відмінники, 11 студентів навчаються на «4» і «5».
|

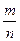 і кажуть що це і є раціональне число. Множину раціональних чисел позначають буквою Q.
і кажуть що це і є раціональне число. Множину раціональних чисел позначають буквою Q.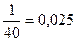 ,
, 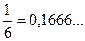 .
.
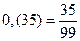 ; б)
; б) 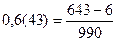 .
.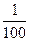 від 500кг кожна, тобто. 17 частин по 5кг. А це становить 85кг. Справедливе також твердження, що 200% від 500кг становить 1000кг, оскільки по відношенню до півтони тонна становить 100% · 2 = 200%.
від 500кг кожна, тобто. 17 частин по 5кг. А це становить 85кг. Справедливе також твердження, що 200% від 500кг становить 1000кг, оскільки по відношенню до півтони тонна становить 100% · 2 = 200%. · 30 = 240 (уч.) або 800 · 0,3 = 240 (уч.).
· 30 = 240 (уч.) або 800 · 0,3 = 240 (уч.).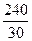 · 100 = 800 (уч.) або 240: 0,3 = 800 (уч.).
· 100 = 800 (уч.) або 240: 0,3 = 800 (уч.). · 100 = 30%.
· 100 = 30%.


