В програмі обов'язково передбачити стирання старих рисунків перед появою нових та додатково - можливість вводу кількості графічних примітивів 9як у В.1.
Варіанти завдань додому
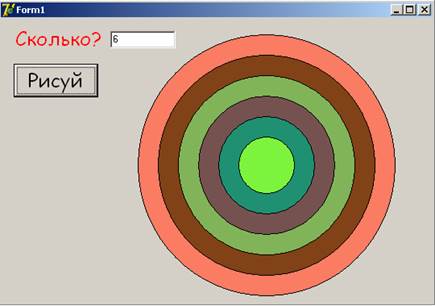
Намалювати круглу мішень.
Координати задамо відносно центра квадратної області, в яку вписаний круг:
Наприклад так: 360-r,180-r - ліва верхня вершина, 360+r,180+r - права нижня вершина квадратної області. r – радіус круга, який зменшуємо r:=r-25;
В 2 Намалювати квадратну мішень.
В 3. Намалювати діаграму та вивести висоту стовпчиків.
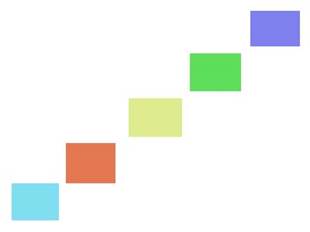
В 4 Намалювати ланцюжок.
На кожному колі вивести його розмір (радіус):
В 5 Намалювати набір прямокутників біля нижнього вивести його розмір.
В 6 Намалювати набір кульок та написати поруч з ними їх розмір
В 7 Намалювати набір прямокутників та написати поруч з ними їх розмір
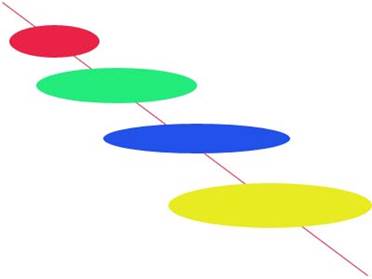
В 8 Намалювати набір еліпсів та написати поруч з ними їх розмір
В 9 Намалювати набір квадратів та написати поруч з ними їх розмір
В 10 Намалювати набір еліпсів та написати поруч з ними їх розмір
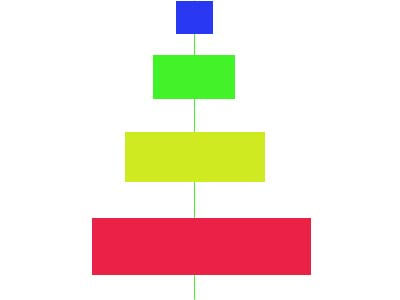
В 11. Створити на формі дитячу пірамідку з n різнокольорових прямокутників, розміри яких крок за кроком зменшуються на 10%.
В 12. Вивести на форму веселку, яка спирається на нижню межу форми.
В 13. Намалювати на формі квадратну сітку, як у зошиті в клітинку.
В 14. Намалювати набір ліній. Написати поруч координату x.
В 15. Намалювати набір ліній.
|

 В 1
В 1