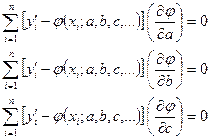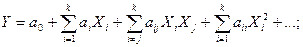Математическое моделирование

Математическое моделирование является типичной дисциплиной, находящейся «на стыке» нескольких наук. Адекватная математическая модель не может быть создана без глубокого знания того объекта, который «обслуживается» математической моделью. Для успешной деятельности в области математического моделирования необходимо знать как математические методы, так и объект моделирования.

Классификация математических моделей на основе особенностей применяемого математического аппарата. В ней можно выделить следующие разновидности.

Математические модели с сосредоточенными параметрами. Обычно с помощью таких моделей описывают динамику систем, состоящих из дискретных элементов. С математической стороны – это системы линейных или нелинейных дифференциальных уравнений. Например, широко используется динамическая модель полупроводникового лазера. В этой модели фигурируют две динамические переменные – концентрация неосновных носителей заряда и фотонов в активной зоне лазера.

В случае сложных систем число динамических переменных и, следовательно, дифференциальных уравнений может быть велико. В этих случаях полезны различные методы редукции системы, основанные на временной иерархии процессов, оценки влияния различных факторов и пренебрежения несущественными среди них и др.

Математические модели с распределенными параметрами. Моделями этого типа описываются процессы диффузии, теплопроводности, распространения волн различной природы и т. п. Эти процессы могут быть не только физической природы. Математические модели с распределёнными параметрами широко распространены в биологии, физиологии и других науках. Чаще всего в качестве основы математической модели применяют уравнения математической физики, в том числе и нелинейные.

Математические модели, основанные на экстремальных принципах. Общеизвестна основополагающая роль принципа наибольшего действия в физике. Экстремальный принцип используется при апроксимации эмпирических зависимостей аналитическим выражением. Графическое изображение такой зависимости и конкретный вид аналитического выражения, описывающий эту зависимость, определяют с помощью экстремального принципа, получившего названия метода наименьших квадратов – метод Гаусса.

Пусть проводится опыт, целью которого является исследование зависимости некоторой физической величины Y от физической величины X. Предполагается, что величины x и y связаны функциональной зависимостью

y = φ (x)

Вид этой зависимости и требуется определить из опыта. Предположим, что в результате опыта получили ряд экспериментальных точек и построили график зависимости y от x (рис. 2). Обычно экспериментальные точки на таком графике располагаются не совсем правильно, дают некоторый разброс, то есть обнаруживают случайные отклонения от видимой общей закономерности. Эти отклонения связаны с неизбежными при всяком опыте ошибками измерения. Тогда возникает типичная для практик задача сглаживания экспериментальной зависимости.

 

Для решения этой задачи обычно применяется расчетный метод, известный под названием метода наименьших квадратов (метод Гаусса). Этот метод дает возможность при заданном типе зависимости y = φ (x) так выбрать её числовые параметры, чтобы кривая y = φ (x) наилучшим образом отображала экспериментальные данные. Вопрос о выборе типа этой кривой часто решается непосредственно по внешнему виду экспериментальной зависимости. Например, экспериментальные точки, изображенные на рис. 2, явно наводят на мысль о прямолинейной зависимости вида y = ax + b. Очень часто вид зависимости (линейная, квадратичная, показательная, и т. д.) бывает известен из физических соображений, связанных с существом решаемой задачи, и из опыта требуется установить только некоторые параметры этой зависимости (коэффициенты).

Вернемся к методу наименьших квадратов. При этом методе требование наилучшего согласования кривой y = φ (x) и экспериментальных точек сводится к тому, что сумма квадратов отклонений экспериментальных точек от сглаживающей кривой обращалась в минимум.

Пусть экспериментальная величина y′ имеет следующие значения: y₁′, y₂′, …y _i ′,… y _n ′, а общий вид функции, зависящий от нескольких числовых параметров a, b, c, … может быть записан как

y = φ (x; a; b; c; …).

Тогда по методу наименьших квадратов требуется выбрать параметры a, b, c, … так, чтобы выполнялось условие

Найдем значения a, b, c, …, обращающие левую часть предыдущего выражения в минимум. Для этого продифференцируем её по a, b, c, … и приравняем производные нулю.

Где (дφ/дa) _i = φ_a ′(x_i; a; b; c; …) — значение частной производной функции φ; по параметру a в точке x_i; остальные производные вычисляются аналогично.

Полученная система уравнений содержит столько же уравнений, сколько неизвестных a, b, c, …

Математические модели в виде интегро-дифференциальных уравнений. Во многих процессах, в которых участвуют большое число объектов, существенную роль играет суммарный результат многих взаимодействий. В этих случаях основу математической модели составляют обычно интегро-дифференциальные уравнения. Примером служит знаменитое уравнение Больцмана, являющееся основой кинетической теории жидкостей и газов.

Разумеется, перечисленные разновидности математических моделей не исчерпывают весь математический аппарат, применяемый в математическом моделировании. Особенно разнообразен математический аппарат теоретической физики и, в частности, её важнейшего раздела – физики элементарных частиц.

Существуют и другие принципы классификации математических моделей.

В качестве такого принципа может выступать область применения математической модели. То есть выделяются следующие области применения:

1. физические процессы;

2. технические приложения, в том числе управляемые системы, искусственный интеллект;

3. жизненные процессы (биология, физиология, медицина);

4. большие системы, связанные с взаимодействием людей (социальные, экономические, экологические);

5. гуманитарные науки (языкознание).

В этих разнообразных применениях математических моделей выделяются определенные общие подходы.

В тоже время существует и значительное своеобразие моделей в отдельных областях их применения. Однако можно отметить, что области применения указанны в порядке, соответствующем убыванию уровня адекватности моделей.

Феноменологические математические модели и модели, отражающие механизм процесса. Между этими двумя разновидностями не существует четкой границы. Как привило, в определенной области науки существует система математических моделей, связанных между собой предельными переходами.

В частности, термодинамика является феноменологической наукой, описывающей поведение сложных систем. Термин «феноменологическая» применен для того, чтобы отразить отказ от рассмотрения молекулярного строения веществ, к описанию которых применена термодинамика.

Таким образом, кинетическая теория газов является феноменологической по отношению к математической модели, в которой взаимодействие между сталкивающимися атомами или молекулами рассматривается в квантово-механическом приближении с учетом их электронной структуры.

Имитационные математические модели. При их создании игнорируются все внутренние особенности моделируемого объекта. Целью моделирования в этом случае является описание объекта – «черного ящика» – как единого целого. Представив в этом случае процесс в виде «черного ящика» находят связь между выходным параметром или параметрами (функциями отклика процесса) и множеством входных управляемых и контролируемых параметров (факторов процесса), отвлекаясь при этом от сущности механизма явлений, протекающих в исследуемом объекте. При этом предполагают, что механизм явления можно описать дифференциальными уравнениями, хотя практически их получить трудно или порой невозможно из-за сложности процесса. Далее предполагают, что систему дифференциальных уравнений можно решить, хотя практически ни решение, ни даже аналитический вид той функции, которой оно задается, как правило, неизвестно.

С учетом принятых предположений, зависимость между функцией отклика любого процесса, представленного в виде «черного ящика», и факторами, действующим на его входе, может быть описана в общем виде полиномом любого порядка:

коэффициенты которого являются коэффициентами ряда Тейлора, то есть значениями частных производных в точке, вокруг которой осуществляется разложение неизвестной функции, задающей решение неизвестных нам дифференциальных уравнений; так a_i=дy/дx_i; a_ji=д²y/дx_iдx_j; a_ii=д²y/дx²_i.

С точки зрения познания механизма явлений, происходящих в исследуемом объекте, имитационная модель представляет собой незначительный интерес. Зная значение первых членов ряда Тейлора, невозможно восстановить исходные дифференциальные уравнения, которым описывается механизм процесса. Правда, возможна физико-механическая интерпретация полученных результатов, но она не дает достаточных представлений о природе явлений. Но, не смотря на все это, полиномиальные модели очень удобны для оптимизации значений функции отклика исследуемого процесса и при планировании эксперимента.

Имитационная модель в виде полинома является математической моделью с сосредоточенными параметрами. В тоже время, для апроксимации эмпирических зависимостей конкретным аналитическим выражением используется экстремальный принцип (метод Гаусса). Поэтому разработанная в итоге математическая модель может быть также отнесена к математическим моделям, основанным на экстремальных принципах. Учитывая, что каждым определённым значениям X будут соответствовать вполне определенные значения Y, то эту модель можно отнести к жестким математическим моделям. Это лишний раз показывает сложность однозначной классификации математических моделей и объясняет многообразие применяемых на практике их классификаций.

В отличие от имитационных моделей, целью математических моделей, претендующих на роль описания теории явления, является адекватное представление объекта на основе фундаментальных законов природы и данных о внутренней структуре моделируемого объекта и взаимодействия его частей.

При выявлении основных, действующих в моделируемом процессе, механизмов очень важен анализ экспериментальных данных и проведение необходимых оценок. Имеются в виду количественные оценки роли различных факторов, которые в итоге должны привести к принципиальной схеме исследуемого процесса, которая составляет основу математической модели.