Определение коэффициента вариации
где С – смещение начала рассеивания показателя надежности При N>25 С=t1-A/2, (6.2) Где А – длина интервала
В первом приближении теоретический закон распределения выбираем по значению коэффициента вариаций: При V<0,3 выбираем закон нормального распределения При V>0,5 выбираем закон распределения Вейбула Для данного примера подходит ЗРВ, но расчет производим по обоим законам.
7.1. Использование для выравнивания распределения опытной информации ЗНР
Закон нормального распределения характеризуется дифференциальной (функцией плотностей вероятностей) и интегральной (функцией распределения) функциями. Отличительная особенность дифференциальной функции – симметричное рассеивание частных значений показателей надежности относительно среднего значения. Дифференциальную функцию описывают уравнением:
где Если принять
Для определения дифференциальной функции через центрированную нормированную функцию используют уравнение:
где А – длина i-того интервала; Кроме того, следует пользоваться уравнением:
Интегральная функция или функция распределения:
Если принять
Для определения интегральной функции
где tKi– значение конца i-того интервала. При этом используют уравнение:
Определим значение интегральной функции, используя таблицу 2.
Таблица 11 - Рассчитанные значения дифференциальной и интегральной функций по всем интервалам статистического ряда
На основании полученных значений f(t) и F(t) строим графики дифференциальной и интегральной функций. Дифференциальная кривая заменяет полигон распределения, а интегральная – кривую накопленных опытных вероятностей.
Рис. 4 – Дифференциальная кривая
Рис. 5 – Интегральная кривая
Определяем количество двигателей, потребующих ремонта в интервале наработки 3056,7…3556,7 мото-ч. Определяем по дифференциальной функции
Количество двигателей
Определяем по интегральной функции
Количество двигателей
7.2. Использование для выравнивания распределения опытной информации ЗРВ Дифференциальную функцию или функцию плотности вероятностей определяют при законе распределения Вейбулла по уравнению:
Где а и b – параметры закона распределения Вейбулла; е – основание натурального логарифма; По таблице №3 методического пособия определяем, что при V=0,54 значения b=1,9;Кb=0,89;Сb=0,49 Параметр а - определяется по уравнению
Дифференциальная функция определяется по таблице №5 методического пособия, при этом используется уравнение:
А– длина интервала статистического ряда; tCi– середина интервала статистического ряда; С– смещение начала рассеяния Рассчитаем дифференциальную функцию:
Интегральная фунция или функция распределения закона Вейбулла определяется по уравнению:
Эту функцию определяем по таблице №6 методического пособия, используя уравнение:
Рассчитаем интегральную функцию:
Таблица 12 - Значения дифференциальной и интегральной функций по всем интервалам статистического ряда
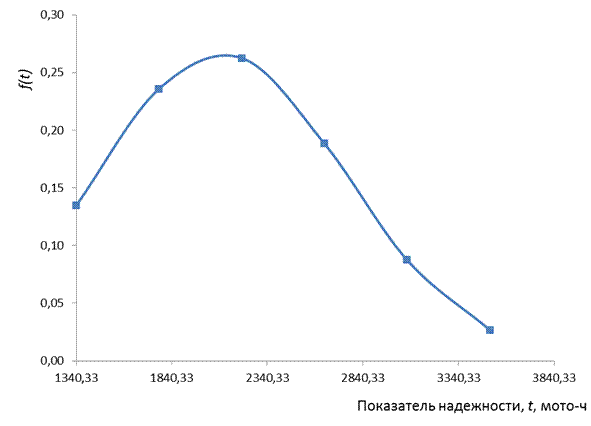
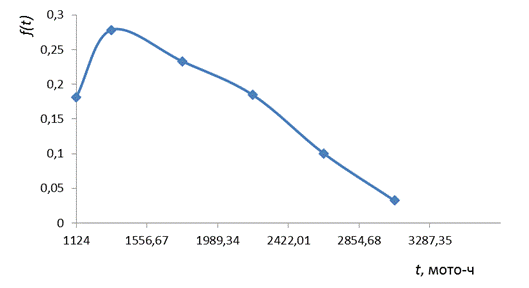
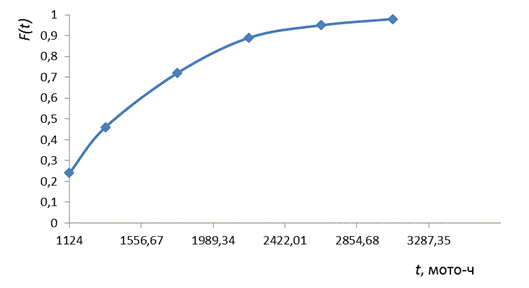
Рис. 6 – Дифференциальная кривая
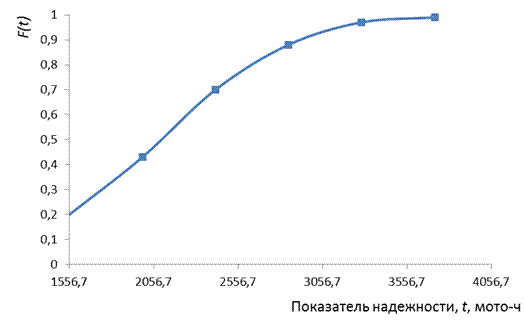
Рис. 7 – Дифференциальная кривая
Определим число двигателей, потребующих ремонта в интервале наработки 3056,7…3556,7 мото-ч По дифференциальной функции
Количество двигателей
По интегральной функции
Количество двигателей
Критерий согласия Пирсона определяется по уравнению:
где ny - число интервалов в укрупненном статистическом ряду; mTi – теоретическая частота в i-ом интервале; mi - опытная частота в i-ом интервале Определяется по уравнению:
где Для определения Проанализировав статистический ряд информации о доремонтных ресурсах двигателя, получаем, что m4=3; m5=2; m6=2, следовательно, необходимо объединить эти интервалы, тогда опытная частота в объединенном интервале будет равна m4=7. В остальных интервалах статистического ряда опытные частоты больше пяти, поэтому эти интервалы оставляем без изменения. Таблица 13 – Укрупненный статистический ряд
Теоретические частоты при ЗНР определяют следующим образом:
Теоретические частоты при ЗРВ:
Тогда критерий согласия Пирсона: - при ЗНР
- при ЗРВ
Вывод: в данном примере выбираем ЗНР т.к Кроме этого пользуясь значениями критерия
где К=3-число обязательных связей.
Значения критериев
Количественные характеристики показателей надежности (среднее значение, среднее квадратическое отклонение, коэффициент вариации), полученные в результате обработки опытной информации, должны быть перенесены на другие совокупности машин, работающие в других режимах и условиях эксплуатации. Однако, несмотря на случайный характер, характеристики показателя надежности рассеиваются в определенных границах. Так, одиночное значение показателя надежности конкретной машины может отличаться в 997 случаях из 1000 от среднего значения Такая высокая степень доверия расчета, охватывающего 99,7% всех случаев, при расчете показателей надежности сельскохозяйственной техники считается излишней. Поэтому степень доверия расчета обычно принимают меньше 99,7% и тем самым сближают границы рассеивания одиночного показателя надежности. Степень доверия расчета на рис.8 оценивают площадью под дифференциальной кривой, ограниченной осью абсцисс и доверительными границами Площадь При расчете доверительных границ рассеивания показателей надежности рекомендуется принимать следующие значения доверительных вероятностей Границы, в которых может колебаться значение одиночного показателя надежности при заданной доверительной вероятности, называют нижней
Рис. 8 – Доверительные границы одиночного и среднего значений показателя надежности 1 и 3 – дифференциальная и интегральная функции одиночного значения; 2 и 4 – дифференциальная и интегральная функции среднего значения
9.1.Определение доверительных границ рассеивания при законе нормального распределения
Определяем абсолютную предельную ошибку переноса опытных характеристик показателя надёжности.
где При β =0,95 и N=28 -
Нижняя доверительная граница равна
где
Верхняя доверительная граница равна
Доверительный интервал
Определение доверительных границ среднего значения показателя надежности при ЗНР Расчетная схема и физический смысл доверительных границ среднего значения показателя надежности те же, что и для одиночного. Разница заключается в значении теоретического среднеквадратического отклонения. Среднее квадратическое отклонение рассеивания среднего значения показателя надежности:
где N– общее число объектов в совокупности Нижняя доверительная граница среднего значения показателя надежности:
Верхняя доверительная граница среднего значения показателя надежности:
Доверительный интервал среднего значения показателя надежности:
9.2.Определение доверительных границ при законе распределения Вейбулла
Доверительные границы рассеивания одиночного значения показателя надежности при ЗРВ определяют по уравнениям:
где а – параметр закона Вейбулла; С – смещение начала рассеивания Доверительный интервал:
Для рассматриваемого примера при доверительной вероятности
Определение доверительных границ рассеивания среднего значения показателя надежности при ЗРВ
Где Доверительный интервал:
Рассчитаем значения при
Наибольшая абсолютная ошибка переноса опытных характеристик показателя надежности при заданной доверительной вероятности равна по значению Относительная предельная ошибка, %
1. Кононенко, А.С. «Методика обработки отказов автотракторных двигателей: методические рекомендации» / А.В. Чепурин, А.С. Кононенко, А.М. Орлов, С.Л. Кушнарев. – М.: УМЦ «ТРИАДА», 2010. – 42 с. 2. Кононенко, А.С. Надежность технических систем. Расчетные уравнения и таблицы: методические рекомендации [Текст] / А.С. Кононенко, А.В. Чепурин, А.М. Орлов, С.Л. Кушнарев. – М.: ФГОУ ВПО МГАУ, 2010. – 26 с.
|

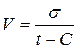 , (6.1)
, (6.1)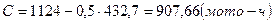
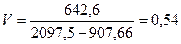
 7. Выбор теоретического закона распределения для выравнивания опытной информации
7. Выбор теоретического закона распределения для выравнивания опытной информации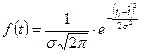 , (7.1)
, (7.1)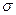 - среднее квадратическое отклонение;
- среднее квадратическое отклонение; 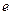 - основание натурального логарифма (
- основание натурального логарифма (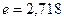 );
);  - значение i-того показателя надежности;
- значение i-того показателя надежности;  - среднее значение показателя надежности.
- среднее значение показателя надежности.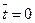 и
и 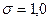 , то получим выражение для центрированной нормированной дифференциальной функции:
, то получим выражение для центрированной нормированной дифференциальной функции: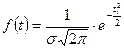 . (7.2)
. (7.2)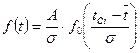 , (7.3)
, (7.3)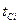 - середина i-того интервала.
- середина i-того интервала.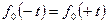 . (7.4)
. (7.4) Определим значение дифференциальной функции, используя таблицу 1.
Определим значение дифференциальной функции, используя таблицу 1.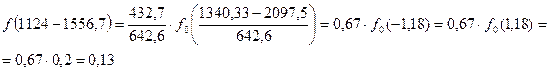
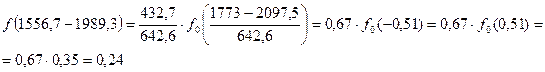
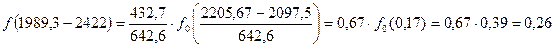
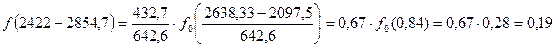
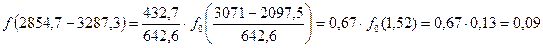
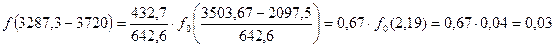
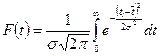 . (7.5)
. (7.5) . (7.6)
. (7.6)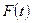 через
через 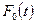 используют уравнение:
используют уравнение: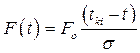 , (7.7)
, (7.7)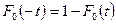 . (7.8)
. (7.8)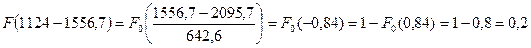
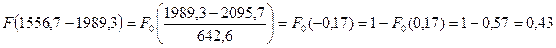

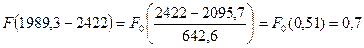
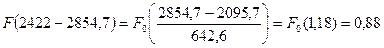
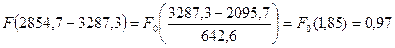
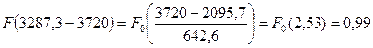

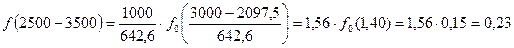
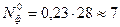
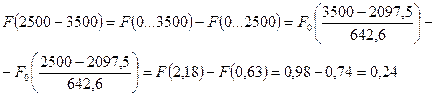
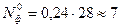
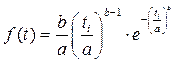 , (7.9)
, (7.9)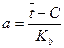 , (7.10)
, (7.10)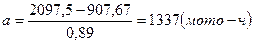
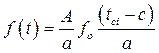 , где (7.11)
, где (7.11)

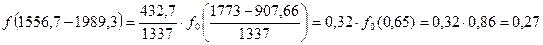
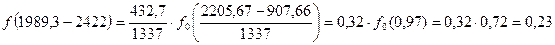

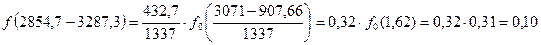
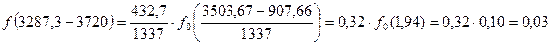
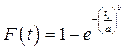 , (7.12)
, (7.12)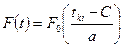 , (7.13)
, (7.13)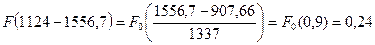
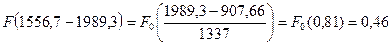

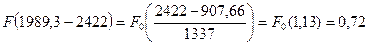
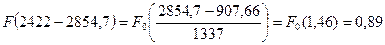
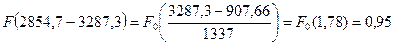
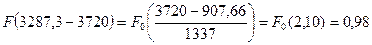
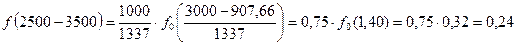
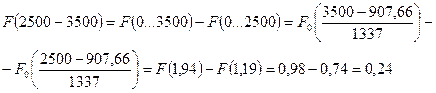

 8. Оценка совпадений опытного и теоретического законов распределения показателя надежности по критерию согласия Пирсона
8. Оценка совпадений опытного и теоретического законов распределения показателя надежности по критерию согласия Пирсона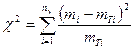 , (8.1)
, (8.1)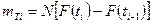 , (8.2)
, (8.2)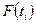 и
и 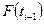 - интегральные функции i-го и (i-1)-того интервалов статистического ряда
- интегральные функции i-го и (i-1)-того интервалов статистического ряда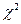 строят укрупненный статистический ряд, при этом соблюдают условие ny>4, mi
строят укрупненный статистический ряд, при этом соблюдают условие ny>4, mi 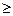 5. При этом допускается объединение соседних интервалов, в которых mi<5.
5. При этом допускается объединение соседних интервалов, в которых mi<5.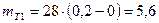
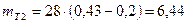
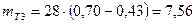

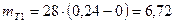
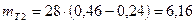
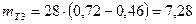
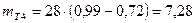
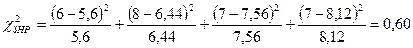

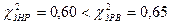
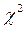 и таблицей №11 определяют вероятность совпадения (Р,%) опытных и теоретических распределений. Для входа в таблицу необходимо определить номер строки.
и таблицей №11 определяют вероятность совпадения (Р,%) опытных и теоретических распределений. Для входа в таблицу необходимо определить номер строки.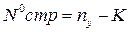
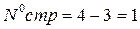

 9. Определение доверительных границ рассеивания одиночного и среднего значения показателя надёжности
9. Определение доверительных границ рассеивания одиночного и среднего значения показателя надёжности на величину
на величину 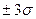 при ЗНР и на величину 0,1а…2,5а при ЗРВ (где а – параметр закона распределения Вейбулла).
при ЗНР и на величину 0,1а…2,5а при ЗРВ (где а – параметр закона распределения Вейбулла).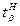 и
и 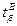 .
. характеризует степень доверия расчета и гарантирует заданную вероятность попадания показателя надежности в соответствующий интервал его значений. Поэтому ее называют доверительной вероятностью
характеризует степень доверия расчета и гарантирует заданную вероятность попадания показателя надежности в соответствующий интервал его значений. Поэтому ее называют доверительной вероятностью 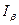 .
.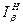 и верхней
и верхней 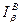 доверительными границами.
доверительными границами.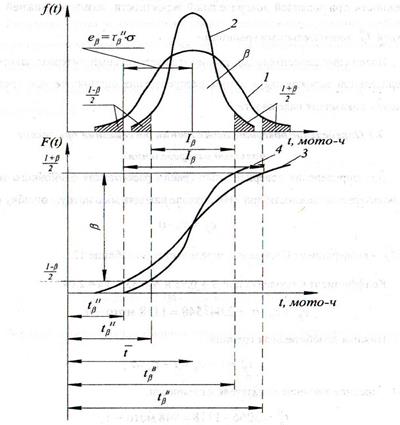
 Положение доверительных границ и доверительный интервал зависят от доверительной вероятности и закона распределения одиночного или среднего значения показателя надежности.
Положение доверительных границ и доверительный интервал зависят от доверительной вероятности и закона распределения одиночного или среднего значения показателя надежности.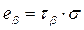 , (9.1)
, (9.1)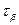 - коэффициент Стьюдента определяется по таблице №12 методического пособия.
- коэффициент Стьюдента определяется по таблице №12 методического пособия.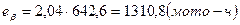
 , (9.2)
, (9.2)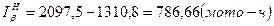
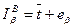 , (9.3)
, (9.3)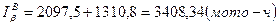
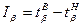 , (9.4)
, (9.4)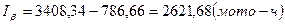
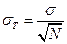 , (9.5)
, (9.5)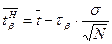 , (9.6)
, (9.6)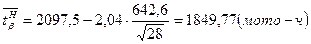
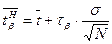 , (9.7)
, (9.7)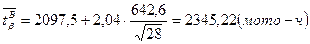
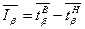 , (9.8)
, (9.8)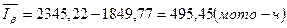

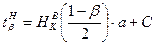 , (9.9)
, (9.9)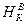 - квантиль закона распределения Вейбулла, определяется по
- квантиль закона распределения Вейбулла, определяется по 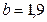
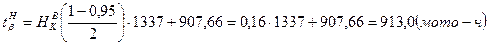


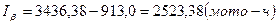
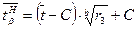 , (9.12)
, (9.12)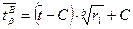 , (9.13)
, (9.13)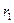 и
и 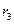 - коэффициенты распределения Вейбулла (таблица 12);
- коэффициенты распределения Вейбулла (таблица 12); 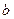 - параметр закона распределения Вэйбулла.
- параметр закона распределения Вэйбулла. и
и 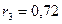 :
: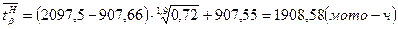
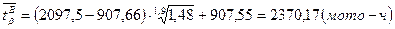
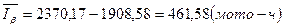
 10. Определение абсолютной и относительной предельных ошибок переноса опытных характеристик показателя надёжности
10. Определение абсолютной и относительной предельных ошибок переноса опытных характеристик показателя надёжности 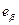 в обе стороны от среднего значения показателя надежности.
в обе стороны от среднего значения показателя надежности.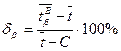 , (10.1)
, (10.1)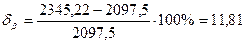
 Список литературы
Список литературы


