ІІ спосіб
Для знаходження матриці
Знайдемо обернену матрицю
Якщо деякий вектор
Але відомо, що Знайдемо координати
Відповідь. Задачі рекомендовані для розв‘язування в аудиторії 1. Вектори а) б) 2. Представити вектор 3. Довести, що кожна з двох даних систем векторів є базисом, і знайти зв'язок між координатами того самого довільно вибраного вектора в цих двох базисах, якщо: а) б) Що відбувається у цьому випадку з координатами вектора при переході від одного базису до іншого? 4. Знайти координати вектора а) б) в ) 5. Довести, що кожна з 2-х заданих систем векторів є базисом, і знайти зв’язок між базисами (матриці переходу від одного базису до іншого). Знайти координати вектора а) б) Задачі для розв'язування дома 1. Вектори а) б) в) 2. Довести, що кожна з двох даних систем векторів є базисом, і знайти зв'язок між координатами того самого довільно вибраного вектора в цих двох базисах, якщо: а) б) 3. Дослідити на лінійну залежність систему векторів: а) б) 4. Знайти координати вектора а) б ) 5. Довести, що кожна з 2-х заданих систем векторів є базисом, і знайти зв’язок між базисами (матриці переходу від одного базису до іншого). Знайти координати вектора а) б) 6. Перевірити, чи утворює кожна із систем векторів базис в просторі a)
|

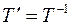 переходу від базису
переходу від базису  до базису В скористаємось формулами:
до базису В скористаємось формулами:
 до матриці
до матриці 
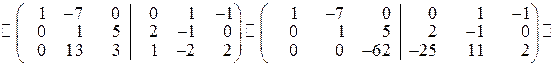
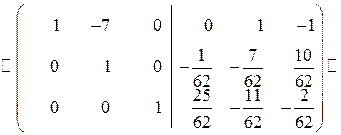

 .
.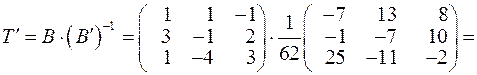
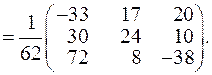
 у базисі
у базисі 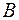 має координатний рядок
має координатний рядок 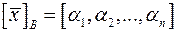 , то в базисі
, то в базисі 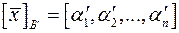 .
.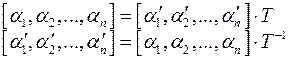
 .
.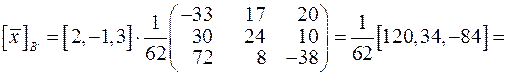

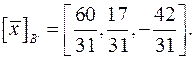
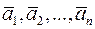 і
і 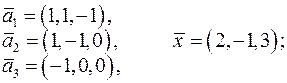
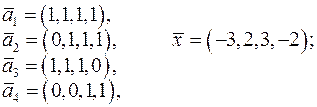
 як лінійну комбінацію векторів
як лінійну комбінацію векторів 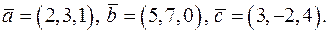


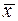 в базисі
в базисі  , якщо він заданий в базисі
, якщо він заданий в базисі  .
.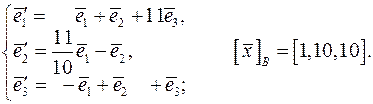
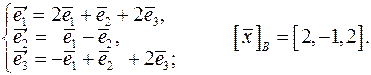



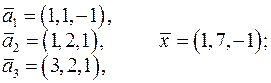

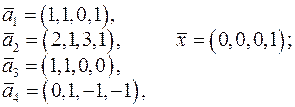
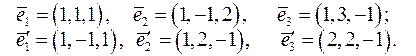
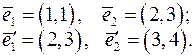
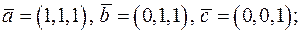

 ;
; .
. в кожному з цих базисів.
в кожному з цих базисів.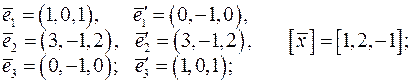

 , і знайти координати вектора
, і знайти координати вектора 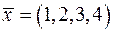 в кожному із цих базисів:
в кожному із цих базисів: ; б)
; б)  ;
; ;
;  ;
; ;
; 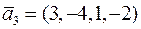 ;
;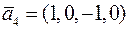 ;
;  .
.


