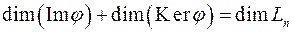Основні теоретичні відомості
Означення 2. Оператор  , який кожному вектору
, який кожному вектору  ставить у відповідність вектор
ставить у відповідність вектор  , називається сумою операторів
, називається сумою операторів  і
і  і записують
і записують 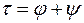 .
.
Отже, 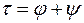 означає, що
означає, що  .
.
[ Тобто  , оператор, який переводить
, оператор, який переводить 
 в суму образів цього вектора ].
в суму образів цього вектора ].
Теорема 2. Сума лінійних операторів є лінійний оператор
Зауваження. Матриця суми лінійних операторів дорівнює сумі матриць лінійних операторів.
Означення 3. Добутком лінійних операторів  і
і  називається такий третій оператор
називається такий третій оператор  , який визначається формулою
, який визначається формулою
 ,
,
де  , і записують
, і записують  .
.
Означена так дія множення операторів  і
і  полягає в послідовності дії операторів
полягає в послідовності дії операторів  і
і  .
.
Теорема 4. Добуток лінійних операторів – є лінійний оператор.
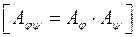
Означення 4. Добутком лінійного оператора  на скаляр
на скаляр  називається оператор, який визначається формулою:
називається оператор, який визначається формулою:
 ],
],
тобто при множенні оператора на скаляр, образ кожного вектора множиться на цей скаляр 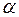 .
.
Теорема 6. Добуток лінійного оператора  на число
на число  є лінійний оператор.
є лінійний оператор.
Властивості  .
.
1. 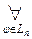
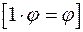 .
.
2. 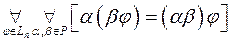 .
.
3.  .
.
4.  .
.
Висновок. Множина 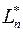 лінійних операторів простору
лінійних операторів простору  з визначеними на цій множині операціями “+” і “
з визначеними на цій множині операціями “+” і “  ”, та множення на скаляр з поля
”, та множення на скаляр з поля  , враховуючи властивості 1 – 4 є лінійним векторним простором над полем
, враховуючи властивості 1 – 4 є лінійним векторним простором над полем  .
.
Якщо лінійним операторам  і
і  відповідають матриці
відповідають матриці  і
і  , то
, то
матриця суми лінійних операторів у довільно вибраному базисі  дорівнює сумі матриць доданків у тому ж базисі
дорівнює сумі матриць доданків у тому ж базисі
 ;
;
матриця добутку лінійних операторів у довільно вибраному базисі  дорівнює добутку матриць співмножників у тому ж базисі
дорівнює добутку матриць співмножників у тому ж базисі
 ;
;
матриця добутку  лінійного оператора
лінійного оператора  на деяке число
на деяке число  у довільно вибраному базисі дорівнює добутку матриці оператора
у довільно вибраному базисі дорівнює добутку матриці оператора  в тому ж базисі на число
в тому ж базисі на число 
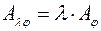 .
.
Область значень і ядро лінійного оператора
Нехай 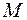 – деяка підмножина
– деяка підмножина  ,
,  – лінійний оператор в
– лінійний оператор в  .
.  Сукупність образів усіх векторів з множини
Сукупність образів усіх векторів з множини 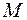 назвали образом множини
назвали образом множини 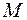 відносно оператора
відносно оператора  і позначили
і позначили 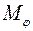 .
.
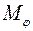 не міститься в
не міститься в 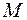 .
.
Теорема 8. Образ кожного лінійного підпростору  простору
простору  відносно будь-якого лінійного оператора
відносно будь-якого лінійного оператора  також є лінійний підпростір
також є лінійний підпростір  .
.
Означення 7. Сукупність  образів всіх векторів простору
образів всіх векторів простору  називається областю значень лінійного оператора
називається областю значень лінійного оператора  .
.
Для скорочення область значень лінійного оператора  називають образомлінійного оператора
називають образомлінійного оператора  і позначають
і позначають 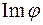 („image” - образ).
(„image” - образ).
Означення 8. Розмірність області значень 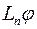 називають рангом оператора
називають рангом оператора  і позначають
і позначають 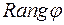 .
.
Теорема 9. Ранг будь-якого лінійного оператора простору  дорівнює рангу матриці цього оператора в довільно вибраному базисі
дорівнює рангу матриці цього оператора в довільно вибраному базисі  .
.
Означення 9. Ядром лінійного оператора 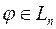 називають сукупність всіх векторів цього простору, що відображаються оператором
називають сукупність всіх векторів цього простору, що відображаються оператором  в нульовий вектор
в нульовий вектор 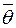 .
.
Ядро оператора  позначають символом Ker
позначають символом Ker  . (“kernel” – ядро).
. (“kernel” – ядро).
Ядро оператора  є лінійний підпростір
є лінійний підпростір  .
.
Означення 10. Розмірність ядра оператора  називають дефектом цього оператора.
називають дефектом цього оператора.
Теорема 10. Сума рангу і дефекту будь-якого лінійного оператора  простору
простору  дорівнює розмірності
дорівнює розмірності 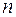 цього простору:
цього простору:
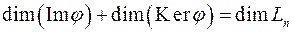

 , який кожному вектору
, який кожному вектору  ставить у відповідність вектор
ставить у відповідність вектор  , називається сумою операторів
, називається сумою операторів  і
і  і записують
і записують 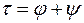 .
. .
. в суму образів цього вектора ].
в суму образів цього вектора ]. , який визначається формулою
, який визначається формулою ,
, .
.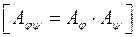
 називається оператор, який визначається формулою:
називається оператор, який визначається формулою: ],
],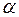 .
. .
.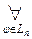
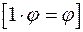 .
.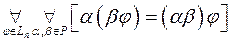 .
. .
. .
.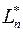 лінійних операторів простору
лінійних операторів простору  з визначеними на цій множині операціями “+” і “
з визначеними на цій множині операціями “+” і “  ”, та множення на скаляр з поля
”, та множення на скаляр з поля  , враховуючи властивості 1 – 4 є лінійним векторним простором над полем
, враховуючи властивості 1 – 4 є лінійним векторним простором над полем  і
і  , то
, то дорівнює сумі матриць доданків у тому ж базисі
дорівнює сумі матриць доданків у тому ж базисі ;
; ;
; лінійного оператора
лінійного оператора  у довільно вибраному базисі дорівнює добутку матриці оператора
у довільно вибраному базисі дорівнює добутку матриці оператора 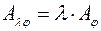 .
.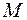 – деяка підмножина
– деяка підмножина  Сукупність образів усіх векторів з множини
Сукупність образів усіх векторів з множини 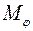 .
. простору
простору  образів всіх векторів простору
образів всіх векторів простору 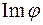 („image” - образ).
(„image” - образ).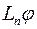 називають рангом оператора
називають рангом оператора 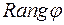 .
.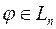 називають сукупність всіх векторів цього простору, що відображаються оператором
називають сукупність всіх векторів цього простору, що відображаються оператором 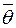 .
.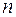 цього простору:
цього простору: