Вироджені і невироджені операториНехай Означення 11. Лінійний оператор Із теореми 10 випливають рівносильні умови невиродженості оператора 1) область значень 2) дефект оператора 3) ядро оператора Теорема 11. Лінійний оператор Теорема 12. Невироджений лінійний оператор Теорема 13. Невироджений лінійний оператор
|
- деякий 
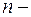вимірний простір, а 
– лінійний оператор 
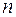; оператор 
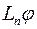оператора 
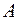в довільно вибраному базисі 
простору 
