Властивості власних векторів та власних чисел.1. У дійсному просторі власними числами будуть лише дійсні корені характеристичного рівняння 2. Якщо всі власні числа матриці різні, то всі її власні вектори лінійно незалежні. 3. Кожному власному вектору відповідає одне власне число. 4. Якщо 5. Якщо 6. Якщо квадратна матриця 7. Якщо квадратна матриця
який називають канонічною формою Жордана матриці
|
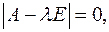а в комплексному просторі – усі корені рівняння 
.
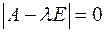- власний вектор матриці 
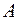з власним числом 
, то будь-який вектор 
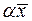, колінеарний вектору 
і 
- власні вектори матриці 
, то їх сума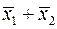 
також є власним вектором матриці 
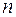має різні власні числа, то матриця 
, рядками якої є власні вектори 
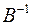
має обернену матрицю 
, то матрицю 
,
