 Нехай
Нехай  – довільний векторний простір і
– довільний векторний простір і  – його одновимірний підпростір;
– його одновимірний підпростір;  – лінійний оператор простору
– лінійний оператор простору  . Одновимірний підпростір породжується будь-яким своїм ненульовим вектором. Отже,
. Одновимірний підпростір породжується будь-яким своїм ненульовим вектором. Отже,  – сукупність векторів виду:
– сукупність векторів виду:  . З геометричної точки зору
. З геометричної точки зору  – це пряма
– це пряма
Якщо підпростір  інваріантний відносно оператора
інваріантний відносно оператора  , то
, то  , тобто
, тобто  , де
, де  .
.
Отже, 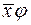 колінеарний
колінеарний  .
.
Означення 14. Вектор  , що задовольняє співвідношення
, що задовольняє співвідношення  , де,
, де,  називається власним вектором оператора
називається власним вектором оператора  , а число
, а число 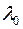 – власним значенням оператора
– власним значенням оператора  , що відповідає власному вектору
, що відповідає власному вектору  .
.
Інакше кажучи,  називається власним вектором оператора
називається власним вектором оператора  , якщо оператор
, якщо оператор  переводить вектор
переводить вектор  в колінеарний (пропорційний) йому вектор:
в колінеарний (пропорційний) йому вектор:  .
.
Для відшукання інваріантних відносно лінійного оператора  одновимірних підпросторів достатньо вміти знаходити власні вектори лінійного оператора
одновимірних підпросторів достатньо вміти знаходити власні вектори лінійного оператора  простору
простору  .
.
Теорема 16. Власні вектори  лінійного оператора
лінійного оператора  , яким відповідають попарно різні власні значення
, яким відповідають попарно різні власні значення  утворюють лінійно незалежну систему.
утворюють лінійно незалежну систему.

 Нехай
Нехай  – довільний векторний простір і
– довільний векторний простір і  – його одновимірний підпростір;
– його одновимірний підпростір;  – лінійний оператор простору
– лінійний оператор простору  . З геометричної точки зору
. З геометричної точки зору  , тобто
, тобто  , де
, де  .
.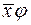 колінеарний
колінеарний  .
. , що задовольняє співвідношення
, що задовольняє співвідношення  , де,
, де,  називається власним вектором оператора
називається власним вектором оператора 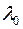 – власним значенням оператора
– власним значенням оператора  лінійного оператора
лінійного оператора  утворюють лінійно незалежну систему.
утворюють лінійно незалежну систему.


