1. Нехай 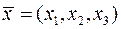 і
і  та
та  – лінійні оператори простору
– лінійні оператори простору 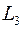 .
. 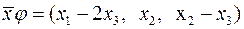 ,
, 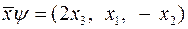 . Знайти координати векторів та їх матриці в тому ж базисі.
. Знайти координати векторів та їх матриці в тому ж базисі.
1.  ; 2.
; 2. 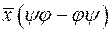 ;
;
3. 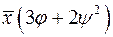 ; 4.
; 4.  ;
;
5. 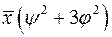 ; 6.
; 6. 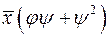
2. Лінійний оператор  векторного простору
векторного простору 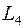 над полем дійсних чисел
над полем дійсних чисел 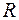 у деякому базисі
у деякому базисі 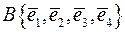 цього простору задано матрицю
цього простору задано матрицю  . Знайти ранг
. Знайти ранг 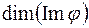 і дефект
і дефект  цього лінійного оператора
цього лінійного оператора  . Побудувати ядро
. Побудувати ядро 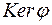 і область значень
і область значень 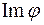 оператора
оператора  .
.
а) 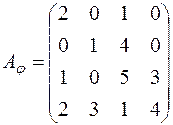 ; б)
; б) 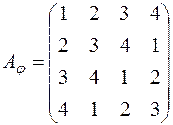 ; в)
; в) 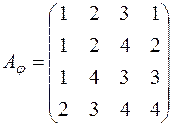 ;
;
г)  ; д)
; д) 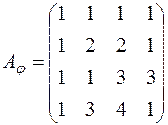 ; е)
; е) 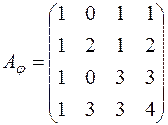 ;
;
є)  ; ж)
; ж)  ; з)
; з)  .
.
3. Лінійний оператор  в базисі
в базисі 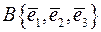 задано матрицею
задано матрицею  . Встановити, чи є
. Встановити, чи є  невиродженим і якщо так, то знайти матрицю. Оберненого оператора
невиродженим і якщо так, то знайти матрицю. Оберненого оператора 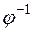 .
.
а) 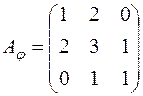 ; б)
; б)  ; в)
; в)  ;
;
г)  ; д)
; д) 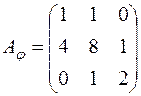 ; е)
; е) 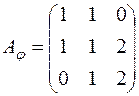 ;
;
є)  ; ж)
; ж) 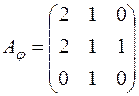 ; з)
; з) 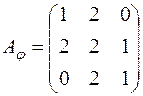 .
.
4. Лінійний оператор  у деякому базисі
у деякому базисі  має матрицю
має матрицю  . Знайти характеристичні корені матриці
. Знайти характеристичні корені матриці  .
.
а) 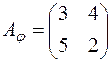 ; б)
; б) 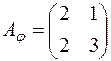 ; в)
; в)  ;
;
г) 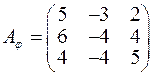 ; д)
; д)  ; е)
; е) 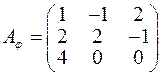 .
.
5. Знайти власні значення та власні вектори лінійного оператора  , заданого матрицею
, заданого матрицею  . З’ясувати, чи складають базис власні вектори простору
. З’ясувати, чи складають базис власні вектори простору 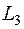 і якщо так, то записати матрицю оператора
і якщо так, то записати матрицю оператора  в цьому базисі.
в цьому базисі.
а) 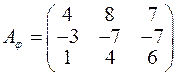 ; б)
; б) 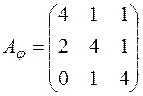 ; в)
; в) 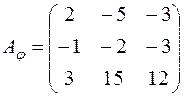 ;
;
г)  ; д)
; д) 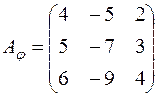 ; е)
; е) 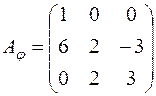 .
.
6. В базисі 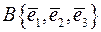 простору
простору 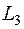 оператор
оператор  задано матрицею
задано матрицею  .
.
а) знайти всі підпростори  простору
простору 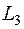 , інваріантні відносно оператора
, інваріантні відносно оператора  ;
;
б) чи має  простий спектр, і якщо так, то знайти базис, в якому
простий спектр, і якщо так, то знайти базис, в якому  зводиться до діагонального вигляду, вказати цю матрицю.
зводиться до діагонального вигляду, вказати цю матрицю.
а) 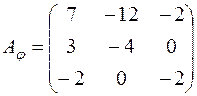 ; б)
; б)  ; в)
; в) 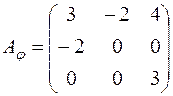 .
.
г) 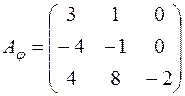 ; д)
; д) 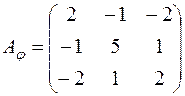 ; е)
; е) 

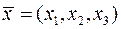 і
і  та
та  – лінійні оператори простору
– лінійні оператори простору 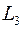 .
. 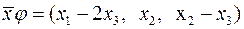 ,
, 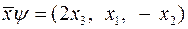 . Знайти координати векторів та їх матриці в тому ж базисі.
. Знайти координати векторів та їх матриці в тому ж базисі. ; 2.
; 2. 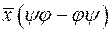 ;
;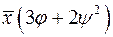 ; 4.
; 4.  ;
;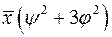 ; 6.
; 6. 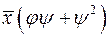
 над полем дійсних чисел
над полем дійсних чисел 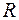 у деякому базисі
у деякому базисі 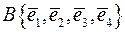 цього простору задано матрицю
цього простору задано матрицю  . Знайти ранг
. Знайти ранг 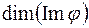 і дефект
і дефект  цього лінійного оператора
цього лінійного оператора 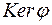 і область значень
і область значень 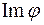 оператора
оператора 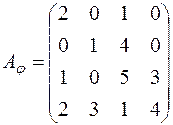 ; б)
; б) 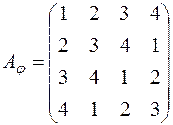 ; в)
; в) 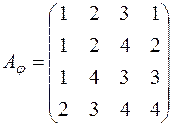 ;
; ; д)
; д) 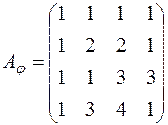 ; е)
; е) 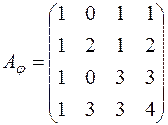 ;
; ; ж)
; ж)  ; з)
; з)  .
.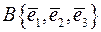 задано матрицею
задано матрицею  . Встановити, чи є
. Встановити, чи є 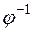 .
.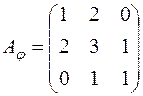 ; б)
; б)  ; в)
; в)  ;
; ; д)
; д) 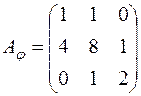 ; е)
; е) 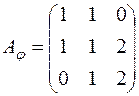 ;
; ; ж)
; ж) 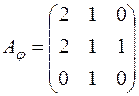 ; з)
; з) 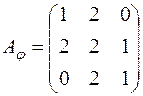 .
. має матрицю
має матрицю 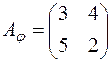 ; б)
; б) 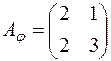 ; в)
; в)  ;
;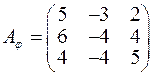 ; д)
; д)  ; е)
; е) 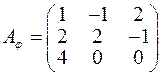 .
.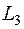 і якщо так, то записати матрицю оператора
і якщо так, то записати матрицю оператора 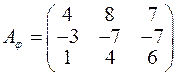 ; б)
; б) 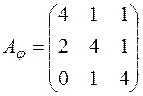 ; в)
; в) 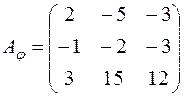 ;
; ; д)
; д) 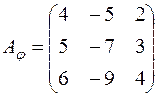 ; е)
; е) 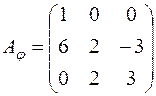 .
. простору
простору 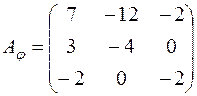 ; б)
; б)  ; в)
; в) 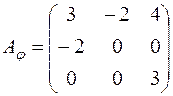 .
.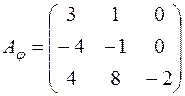 ; д)
; д) 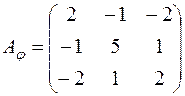 ; е)
; е) 



