Лінійні оператори з простим спектром.

Серед лінійних операторів найпростіші є ті, які мають простий спектр.

Теорема 18. Якщо вектори базису є власними векторами лінійного оператора , то в базисі оператор задається діагональною матрицею. Навпаки, якщо в деякому базисі матриця оператора є діагональною, то всі вектори цього базису є власними векторами оператора .

Теорема 19. Для того, щоб в лінійному просторі лінійний оператор мав базис із власних векторів, необхідно і достатньо, щоб всі характеристичні числа 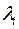оператора належали основному полю, і щоб кожному числу 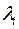відповідало стільки лінійно незалежних власних векторів оператора , яка алгебраїчна кратність кореня 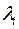характеристичного многочленна оператора .

Для того, щоб матриця була матрицею простої структури, тобто, щоб вона зводилась до діагонального вигляду, необхідно і достатньо, щоб всі характеристичні корені 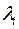матриці належали основному полю і щоб для кожного кореня 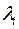його геометрична кратність ( - ранг матриці ) співпадала з алгебраїчною кратністю 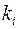, тобто з кратністю кореня 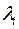характеристичного многочлена 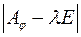матриці .

Теорема 20. Якщо лінійний оператор має простий спектр, то існує базис простору , в якому цей оператор задається діагональною матрицею.