Теорема 21. Кожна квадратна матриця 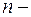 го порядку над полем
го порядку над полем  , яка має у полі
, яка має у полі 
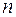 різних характеристичних коренів, подібна до деякої діагональної матриці, тобто зводиться до діагонального вигляду.
різних характеристичних коренів, подібна до деякої діагональної матриці, тобто зводиться до діагонального вигляду.
Методичні рекомендації до розв‘язування задач
Приклад 1. 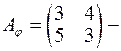 матриця оператора
матриця оператора  в базисі
в базисі 
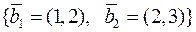 ;
; 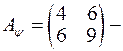 матриця оператора
матриця оператора  в базисі
в базисі 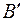
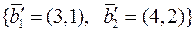 . Знайти матрицю оператора
. Знайти матрицю оператора  в базисі
в базисі 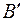
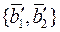 .
.
Розв’язання. Позначимо матрицю оператора  :
:  , тоді в базисі
, тоді в базисі 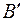 :
: 
 , де
, де  - матриця оператора
- матриця оператора  в базисі
в базисі 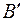
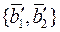 . За формулою
. За формулою  , де
, де 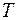 - матриця переходу від базису
- матриця переходу від базису  до базису
до базису 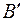 . Обчислимо
. Обчислимо 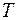 .
.
 ,
, 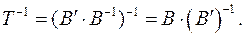
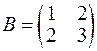 ,
,  ,
, 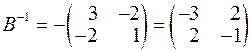 .
.
 ,
,  ,
,  .
.
Тоді
 .
.
 .
.
Обчислимо

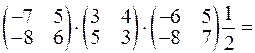
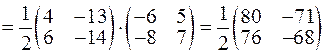 .
.
Отже,
 .
.
Відповідь: 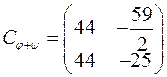 .
.
Приклад 2. Лінійний оператор  в базисі
в базисі 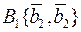 , де
, де  ,
,  має матрицю
має матрицю 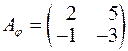 . Лінійний оператор
. Лінійний оператор  в базисі
в базисі  , де
, де 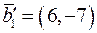 ,
, 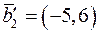 має матрицю
має матрицю  . Знайти
. Знайти 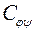 в базисі
в базисі 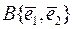 , де
, де  ,
, 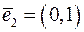 .
.
Розв’язання. Для того, щоб знайти матрицю 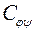 в базисі
в базисі 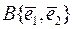 , необхідно обчислити матриці лінійних операторів
, необхідно обчислити матриці лінійних операторів  і
і  в базисі
в базисі 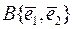 .
.
Обчислимо матриці цих операторів в базисі 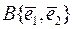 за формулами
за формулами  ,
,  , де
, де  - матриця переходу від базису
- матриця переходу від базису 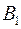 до
до  .
. 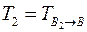 - матриця переходу від базису
- матриця переходу від базису 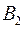 до
до  .
.


 ,
, 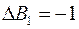 ,
, 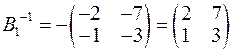 .
. 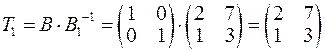 .
.
 .
.
 ,
, 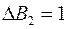 ,
, 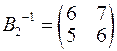 .
.  .
.
Обчислимо  і
і  .
.
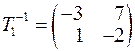 ,
,  .
.
Отже,
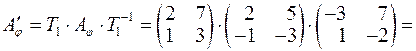
 .
.

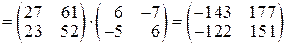 .
.
 .
.
Відповідь:  .
.
Приклад 3. Нехай  і
і  та
та  – лінійні оператори простору
– лінійні оператори простору 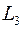 .
.  ,
, 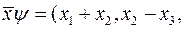
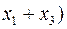 . Знайти: а)
. Знайти: а)  , б)
, б)  , в)
, в)  .
.
Розв’язання. При розв’язуванні задачі скористаємося означенням суми та добутку лінійних операторів:
 ;
;
 .
.
а)  ,
,
 ,
,
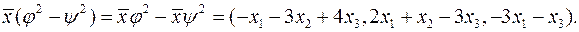 Матриця цього перетворення має вигляд:
Матриця цього перетворення має вигляд:
 .
.
Другий спосіб. Знайдемо матриці перетворення лінійних операторів  і
і  .
.
 ,
,  .
.
Виконаємо перетворення:
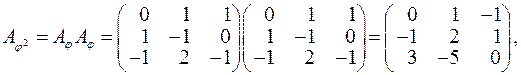
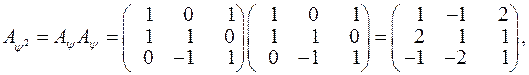
 Відповідь:
Відповідь:  .
.
 .
.
б) 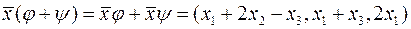


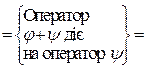


 .
.
 ;
;
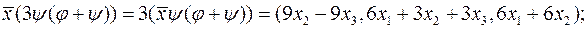
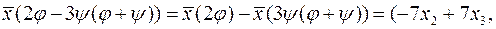
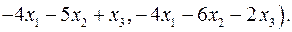
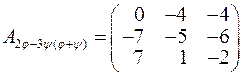 .
.
Другий спосіб.
Розглянемо 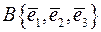 , де
, де 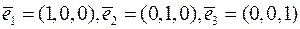 . Подіємо лінійними операторами
. Подіємо лінійними операторами  та
та  на вектори базису
на вектори базису 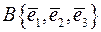
 ,
,  ,
,
 ,
, 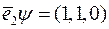 ,
,
 ;
; 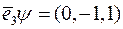 .
.
 і
і  .
.
Тоді
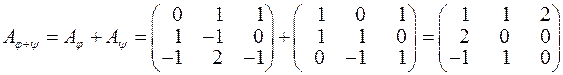 .
.
За означенням, матриця добутку лінійних операторів дорівнює добутку матриць лінійних операторів.
 .
.

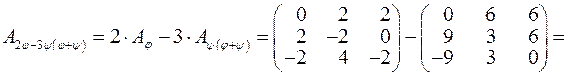
 .
.
Відповідь: 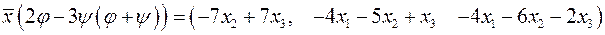 ;
;

 .
.
в) 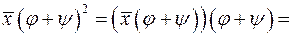
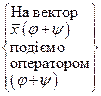
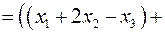


 .
.
Матриця цього перетворення має вигляд:
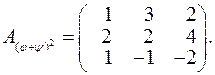
Другий спосіб.
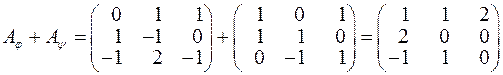 .
.
 .
.
Відповідь: 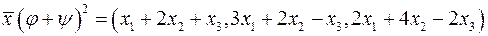 ,
,
 .
.
Приклад 4. Нехай  і
і  та
та  – лінійні оператори простору
– лінійні оператори простору 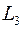 .
.  ,
,  .. Знайти
.. Знайти  в тому ж базисі.
в тому ж базисі.
Розв’язання. I. За означеннями дій над лінійними операторами, знаходимо:
 ,
,
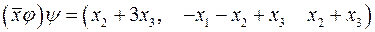 . { оператор
. { оператор  діє на вектор
діє на вектор 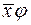 }.
}.
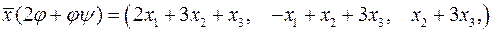 .
.
Знайдемо матрицю, яка відповідає результату дій над даними лінійними операторами:
 .
.
II. Знайдемо матриці операторів  і
і  :
:
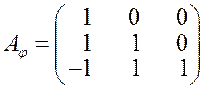 ,
,  .
.
За правилами множення матриць, додавання матриць і множення матриці на число, обчислюємо:

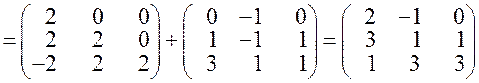 .
.
Знайдемо координатний рядок образа вектора  , якщо діє оператор
, якщо діє оператор 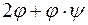 .
.
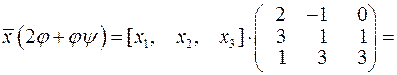 .
.
 .
.
Відповідь:
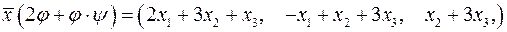 ,
, 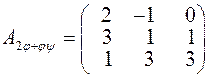 .
.
Приклад 5. Нехай лінійний оператор  векторного простору
векторного простору 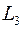 над полем дійсних чисел
над полем дійсних чисел 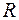 у деякому базисі
у деякому базисі 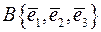 цього простору задано матрицею: а)
цього простору задано матрицею: а) 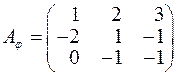 , б)
, б) 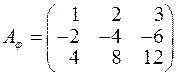 ,
,
в) 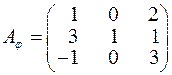 . Знайти ранг
. Знайти ранг 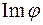 і дефект
і дефект  лінійного оператора
лінійного оператора  . Побудувати ядро
. Побудувати ядро  і область значень
і область значень 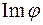 оператора
оператора  .
.
Розв’язання.
а) Оскільки ранг  лінійного оператора
лінійного оператора  простору
простору 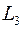 дорівнює рангу
дорівнює рангу  матриці
матриці  цього оператора в базисі
цього оператора в базисі 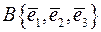 , то знаходимо спочатку
, то знаходимо спочатку  :
:
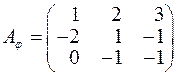
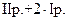 ~
~  IIp+5·IIIp ~
IIp+5·IIIp ~ 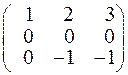 .
.
Звідси 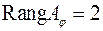 і тому
і тому  .
.
Внаслідок того, що сума рангу і дефекту довільного лінійного оператора векторного простору дорівнює розмірності цього простору, то  ,
, 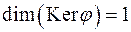 .
.
Для побудови ядра  і області значень
і області значень 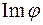 оператора
оператора  досить визначити їх базиси.
досить визначити їх базиси.
Оскільки область значень 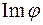 оператора
оператора  складається з образів усіх векторів простору
складається з образів усіх векторів простору 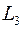 , тобто з усіх векторів виду
, тобто з усіх векторів виду 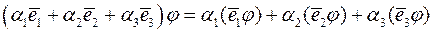 , де
, де  , то підпростір
, то підпростір 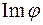 породжується системою векторів
породжується системою векторів 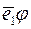 ,
,  ,
,  . (а)
. (а)
Отже, за базис підпростору 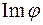 можна взяти довільну максимальну лінійно незалежну підсистему векторів системи (а).
можна взяти довільну максимальну лінійно незалежну підсистему векторів системи (а).
Оскільки
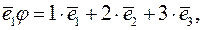
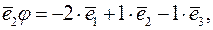
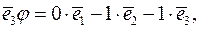
то такі підсистеми визначаються максимальними лінійно незалежними підсистемами рядків матриці  . Із знаходження рангу матриці
. Із знаходження рангу матриці  видно, що однією з максимальних лінійно незалежних підсистем рядків цієї матриці є підсистема, яка складається з першого та третього рядків матриці. Тоді за базис підпростору
видно, що однією з максимальних лінійно незалежних підсистем рядків цієї матриці є підсистема, яка складається з першого та третього рядків матриці. Тоді за базис підпростору 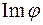 можна взяти вектори
можна взяти вектори 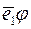 ,
,  .
.
Побудуємо ядро  лінійного оператора
лінійного оператора  . Оскільки вектор
. Оскільки вектор  належить до ядра
належить до ядра  оператора
оператора  тоді і тільки тоді, коли
тоді і тільки тоді, коли  , тобто коли
, тобто коли 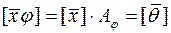 , де
, де 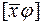 і
і  - координатні рядки векторів
- координатні рядки векторів 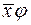 і
і  в базисі
в базисі 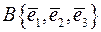 , то
, то  є множина всіх тих векторів простору
є множина всіх тих векторів простору 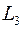 , координатні рядки яких у базисі
, координатні рядки яких у базисі 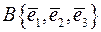 , розглядувані як числові вектори, утворюють простір розв’язків такої системи лінійних однорідних рівнянь
, розглядувані як числові вектори, утворюють простір розв’язків такої системи лінійних однорідних рівнянь 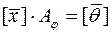 , або в розгорнутому вигляді
, або в розгорнутому вигляді
 (б)
(б)
Оскільки матриця останньої системи є матрицею, транспонованою до матриці  , то, використовуючи процес знаходження рангу матриці
, то, використовуючи процес знаходження рангу матриці  , можна стверджувати, що ранг цієї системи дорівнює числу 2 і що за вільне невідоме можна взяти
, можна стверджувати, що ранг цієї системи дорівнює числу 2 і що за вільне невідоме можна взяти  . Тоді
. Тоді 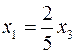 ,
, 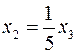 - загальний розв’язок системи (б), а
- загальний розв’язок системи (б), а  =
=  – фундаментальна система розв’язків системи (б), яка є базисом простору
– фундаментальна система розв’язків системи (б), яка є базисом простору  .
.
Зауваження. Надалі, розв’язуючи такі задачі, ми спрощуватимемо процес розв’язання, а саме:
1. Знайдемо ранг 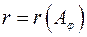 матриці
матриці  . Це буде розмірність
. Це буде розмірність  області значень
області значень 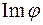 заданого оператора
заданого оператора  . Тоді розмірність
. Тоді розмірність  ядра
ядра  оператора
оператора  знайдемо з рівності
знайдемо з рівності 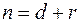 , де
, де 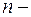 розмірність усього простору.
розмірність усього простору.
2. Визначимо базис 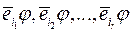 простору
простору 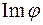 . Тут
. Тут  – номери тих рядків матриці
– номери тих рядків матриці  , які складають максимальну лінійно незалежну систему рядків цієї матриці (зрозуміло, що числа
, які складають максимальну лінійно незалежну систему рядків цієї матриці (зрозуміло, що числа  визначаються неоднозначно).
визначаються неоднозначно).
3. Знайдемо фундаментальну систему розв’язків  системи лінійних однорідних рівнянь, матрицею якої є матриця, транспонована до матриці
системи лінійних однорідних рівнянь, матрицею якої є матриця, транспонована до матриці  . Базис простору
. Базис простору  і буде
і буде  (
( також, очевидно, визначається однозначно).
також, очевидно, визначається однозначно).
б) 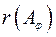 =?
=?
 ,
,  .
.
Отже,
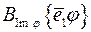 , де
, де 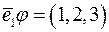 .
.

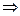 базис
базис  складається із двох векторів.
складається із двох векторів.
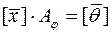
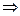
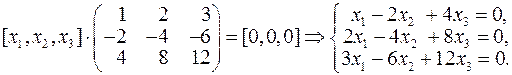
Загальний розв’язок останньої системи:  . Фундаментальна система розв’язків останньої системи складається із векторів
. Фундаментальна система розв’язків останньої системи складається із векторів 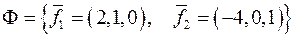 .
.
Отже, базис  складається із векторів
складається із векторів 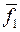 і
і  .
.  .
.
в) 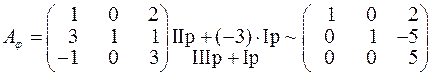 ,
,  .
.
Отже,  , де
, де  ,
,  ,
, 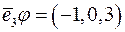 .
. 
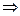 базис
базис  складається з
складається з 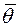 .
.
Приклад 6. Лінійний оператор  в базисі
в базисі 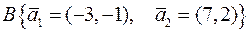 має матрицю
має матрицю 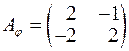 , а лінійний оператор
, а лінійний оператор  в базисі
в базисі  має матрицю
має матрицю  . Знайти матриці лінійних операторів
. Знайти матриці лінійних операторів  та
та  в базисі, в якому задано координати всіх векторів.
в базисі, в якому задано координати всіх векторів.
Розв’язання. Введемо позначення 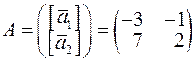 ,
, 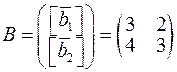 для заданих базисів і
для заданих базисів і 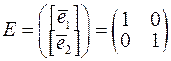 для базису, в якому задано координати векторів. Завдання полягає в тому, щоб знайти матриці, що відповідають добуткам лінійних операторів
для базису, в якому задано координати векторів. Завдання полягає в тому, щоб знайти матриці, що відповідають добуткам лінійних операторів  та
та  .
.
Матрицю лінійного оператора  в базисі
в базисі 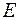 позначимо
позначимо  , а оператора
, а оператора  -
- 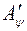 .
.
Тоді
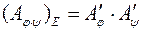 і
і 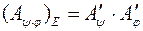 .
.
За формулою обчислення матриці лінійного оператора в іншому базисі:
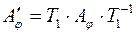 і
і 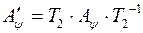 , де
, де 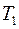 і
і  - матриці переходу від базисів
- матриці переходу від базисів  і
і 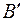 до базису
до базису 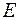 відповідно.
відповідно.
Оскільки матриці 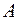 і
і  , рядки яких складено відповідно з координатних рядків векторів
, рядки яких складено відповідно з координатних рядків векторів  і
і  , є матрицями переходу від базису
, є матрицями переходу від базису 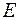 до базисів
до базисів  і
і 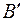 відповідно, то, враховуючи зв'язок між матрицями переходу від одного базису до іншого, дістанемо рівності
відповідно, то, враховуючи зв'язок між матрицями переходу від одного базису до іншого, дістанемо рівності
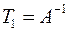 ,
, 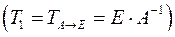 ;
;
 ,
, 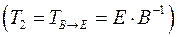 .
.
Тоді
 і
і  .
.
Обчислимо послідовно:
 ,
,  .
.
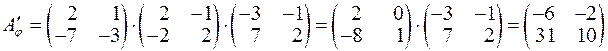 .
.
 .
.
Обчислюємо шукані матриці:
 .
.
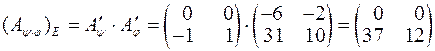 .
.
Відповідь: 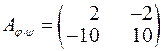 ,
,  .
.
Приклад 7. В лінійному просторі  заданий базис
заданий базис 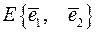 . Лінійний оператор
. Лінійний оператор  переводить вектори
переводить вектори  з координатами
з координатами 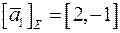 ,
,  відповідно у вектори
відповідно у вектори  з координатами
з координатами  ,
, 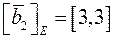 . Знайти матрицю оператора
. Знайти матрицю оператора  в базисі
в базисі 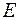 .
.
Розв’язання. Через  позначимо оператор, який переводить вектори
позначимо оператор, який переводить вектори  у вектори
у вектори  . Його матрицею у базисі
. Його матрицею у базисі 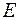 буде
буде
 .
.
Оператор  переводить вектори
переводить вектори  у вектори
у вектори  . Отже, добуток
. Отже, добуток  операторів
операторів  і
і  переводить вектори
переводить вектори  у вектори
у вектори  . Тому в базисі
. Тому в базисі 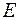 оператор
оператор  має матрицю
має матрицю
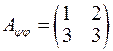 .
.
Матриця  оператора
оператора  дорівнює добутку матриць операторів
дорівнює добутку матриць операторів  і
і  , тобто якщо
, тобто якщо  - матриця оператора
- матриця оператора  в базисі
в базисі 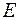 , то
, то 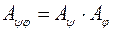 . Тоді маємо:
. Тоді маємо: 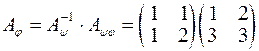
Відповідь:  - матриця оператора
- матриця оператора  в базисі
в базисі 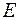 .
.

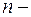 го порядку над полем
го порядку над полем  , яка має у полі
, яка має у полі 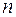 різних характеристичних коренів, подібна до деякої діагональної матриці, тобто зводиться до діагонального вигляду.
різних характеристичних коренів, подібна до деякої діагональної матриці, тобто зводиться до діагонального вигляду.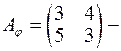 матриця оператора
матриця оператора  в базисі
в базисі 
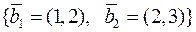 ;
; 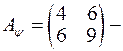 матриця оператора
матриця оператора  в базисі
в базисі 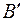
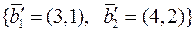 . Знайти матрицю оператора
. Знайти матрицю оператора  в базисі
в базисі 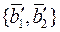 .
. :
:  , тоді в базисі
, тоді в базисі  , де
, де  - матриця оператора
- матриця оператора  , де
, де 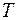 - матриця переходу від базису
- матриця переходу від базису  ,
, 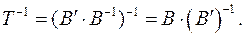
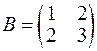 ,
,  ,
, 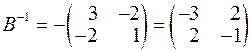 .
. ,
,  ,
,  .
. .
. .
.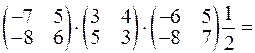
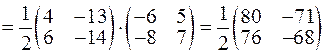 .
. .
.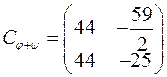 .
.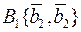 , де
, де  ,
,  має матрицю
має матрицю 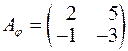 . Лінійний оператор
. Лінійний оператор  , де
, де 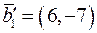 ,
, 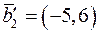 має матрицю
має матрицю  . Знайти
. Знайти 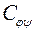 в базисі
в базисі 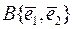 , де
, де  ,
, 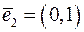 .
. ,
,  , де
, де  - матриця переходу від базису
- матриця переходу від базису 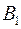 до
до 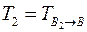 - матриця переходу від базису
- матриця переходу від базису 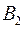 до
до 

 ,
, 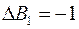 ,
, 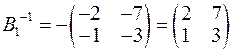 .
. 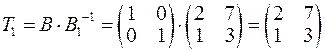 .
. .
. ,
, 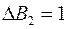 ,
, 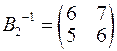 .
.  .
. і
і  .
.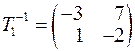 ,
,  .
.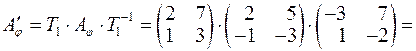
 .
.
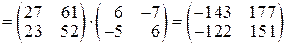 .
. .
. .
. і
і 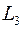 .
.  ,
, 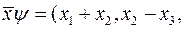
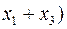 . Знайти: а)
. Знайти: а)  , б)
, б)  , в)
, в)  .
. ;
; .
. ,
, ,
,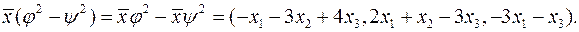 Матриця цього перетворення має вигляд:
Матриця цього перетворення має вигляд: .
. ,
,  .
.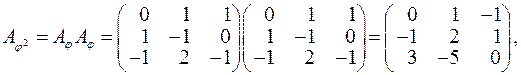
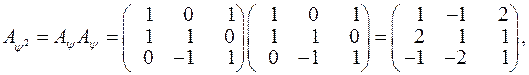
 Відповідь:
Відповідь:  .
.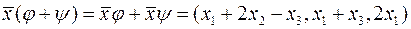

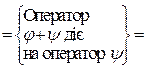


 .
. ;
;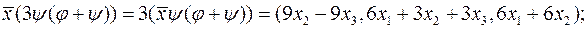
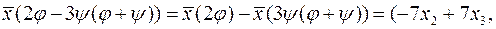
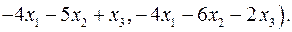
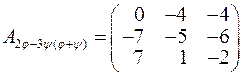 .
.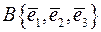 , де
, де 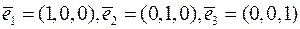 . Подіємо лінійними операторами
. Подіємо лінійними операторами  ,
,  ,
, ,
, 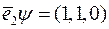 ,
, ;
; 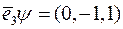 .
.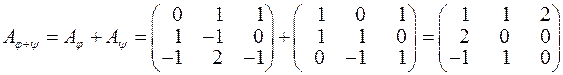 .
. .
.
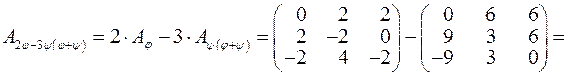
 .
.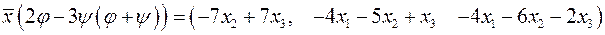 ;
;
 .
.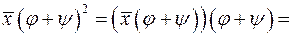
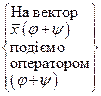
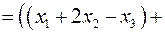


 .
.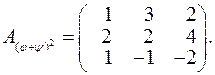
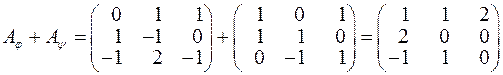 .
. .
.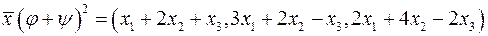 ,
, .
. ,
,  .. Знайти
.. Знайти  в тому ж базисі.
в тому ж базисі. ,
,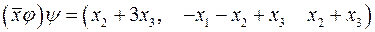 . { оператор
. { оператор 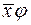 }.
}.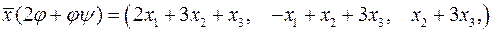 .
. .
.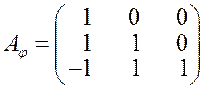 ,
,  .
.
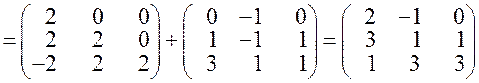 .
. , якщо діє оператор
, якщо діє оператор 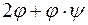 .
.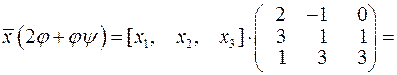 .
. .
.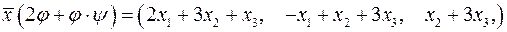 ,
, 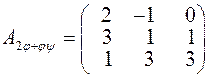 .
.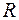 у деякому базисі
у деякому базисі 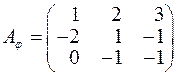 , б)
, б) 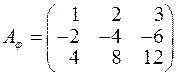 ,
,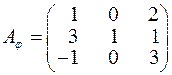 . Знайти ранг
. Знайти ранг 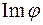 і дефект
і дефект  лінійного оператора
лінійного оператора  лінійного оператора
лінійного оператора  матриці
матриці  цього оператора в базисі
цього оператора в базисі 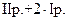 ~
~  IIp+5·IIIp ~
IIp+5·IIIp ~ 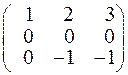 .
.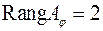 і тому
і тому  .
. ,
, 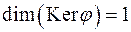 .
.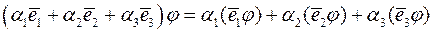 , де
, де  , то підпростір
, то підпростір 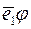 ,
,  ,
,  . (а)
. (а)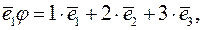
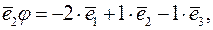
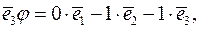
 належить до ядра
належить до ядра  , тобто коли
, тобто коли 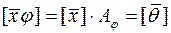 , де
, де 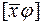 і
і  - координатні рядки векторів
- координатні рядки векторів 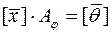 , або в розгорнутому вигляді
, або в розгорнутому вигляді (б)
(б) . Тоді
. Тоді 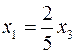 ,
, 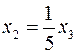 - загальний розв’язок системи (б), а
- загальний розв’язок системи (б), а  =
=  – фундаментальна система розв’язків системи (б), яка є базисом простору
– фундаментальна система розв’язків системи (б), яка є базисом простору 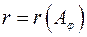 матриці
матриці  ядра
ядра 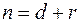 , де
, де 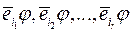 простору
простору  – номери тих рядків матриці
– номери тих рядків матриці 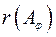 =?
=? ,
,  .
.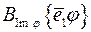 , де
, де 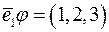 .
.
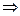 базис
базис 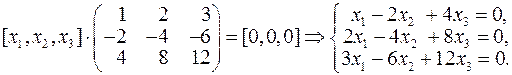
 . Фундаментальна система розв’язків останньої системи складається із векторів
. Фундаментальна система розв’язків останньої системи складається із векторів 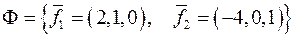 .
.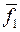 і
і  .
.  .
.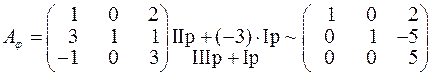 ,
,  .
. , де
, де  ,
,  ,
, 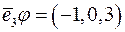 .
. 
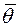 .
.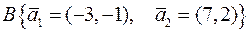 має матрицю
має матрицю 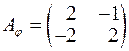 , а лінійний оператор
, а лінійний оператор  має матрицю
має матрицю  . Знайти матриці лінійних операторів
. Знайти матриці лінійних операторів  та
та  в базисі, в якому задано координати всіх векторів.
в базисі, в якому задано координати всіх векторів.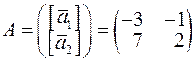 ,
, 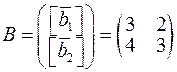 для заданих базисів і
для заданих базисів і 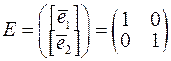 для базису, в якому задано координати векторів. Завдання полягає в тому, щоб знайти матриці, що відповідають добуткам лінійних операторів
для базису, в якому задано координати векторів. Завдання полягає в тому, щоб знайти матриці, що відповідають добуткам лінійних операторів 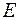 позначимо
позначимо 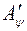 .
.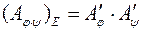 і
і 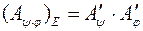 .
.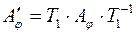 і
і 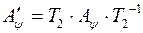 , де
, де 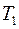 і
і  - матриці переходу від базисів
- матриці переходу від базисів 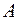 і
і  і
і  , є матрицями переходу від базису
, є матрицями переходу від базису 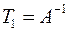 ,
, 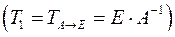 ;
; ,
, 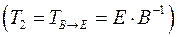 .
. і
і  .
. ,
,  .
.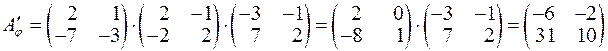 .
. .
. .
.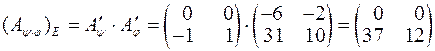 .
.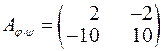 ,
,  .
. заданий базис
заданий базис 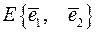 . Лінійний оператор
. Лінійний оператор 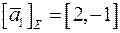 ,
,  відповідно у вектори
відповідно у вектори  ,
, 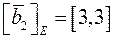 . Знайти матрицю оператора
. Знайти матрицю оператора  у вектори
у вектори  .
.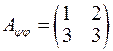 .
. оператора
оператора 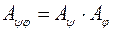 . Тоді маємо:
. Тоді маємо: 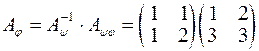
 - матриця оператора
- матриця оператора 


