Характеристичне рівняння лінійного оператора

⇐ Предыдущая 1 2 3 456 7 8 9 10 Следующая ⇒

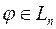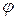Нехай - довільний векторний простір, , . В лінійний оператор визначається матрицею 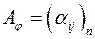, , 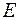– одинична матриця і - деяке невідоме.

Означення 15. Матриця виду 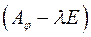називається характеристичною матрицю для , тобто матриця виду:

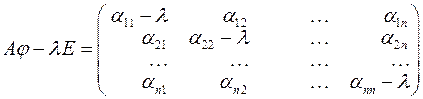а 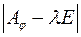називається характеристичним многочленом матриці , корені якого називаються характеристичними коренями цієї матриці: 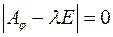– характеристичне рівняння матриці .

Визначник 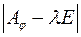матриці 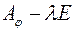є многочленом 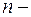го степеня від . (Корені цього многочлена можуть бути як дійсними так і комплексними).

Так як матриці лінійного оператора 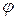в різних базисах подібні, а визначники подібних матриць рівні між собою, то характеристичні рівняння, а отже і характеристичні корені лінійного оператора 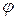однакові.

Означення 16. Сукупність характеристичних коренів лінійного оператора з врахуванням їх кратності називається спектром лінійного оператора 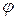. Якщо всі характеристичні корені лінійного оператора 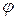різні, то спектр називають простим.

Теорема 17. Для того, щоб число 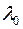з поля було власним значенням лінійного оператора 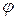, необхідно і достатньо, щоб воно було характеристичним коренем цього оператора.

⇐ Предыдущая 1 2 3 456 7 8 9 10 Следующая ⇒

Дата добавления: 2015-09-07; просмотров: 1095. Нарушение авторских прав; Мы поможем в написании вашей работы!

Композиция из абстрактных геометрических фигур Данная композиция состоит из линий, штриховки, абстрактных геометрических форм...

Важнейшие способы обработки и анализа рядов динамики Не во всех случаях эмпирические данные рядов динамики позволяют определить тенденцию изменения явления во времени...

ТЕОРЕТИЧЕСКАЯ МЕХАНИКА Статика является частью теоретической механики, изучающей условия, при которых тело находится под действием заданной системы сил...

Теория усилителей. Схема Основная масса современных аналоговых и аналого-цифровых электронных устройств выполняется на специализированных микросхемах...

В теории государства и права выделяют два пути возникновения государства: восточный и западный Восточный путь возникновения государства представляет собой плавный переход, перерастание первобытного общества в государство...

Закон Гука при растяжении и сжатии Напряжения и деформации при растяжении и сжатии связаны между собой зависимостью, которая называется законом Гука, по имени установившего этот закон английского физика Роберта Гука в 1678 году...

Характерные черты официально-делового стиля Наиболее характерными чертами официально-делового стиля являются: • лаконичность...

Дезинфекция предметов ухода, инструментов однократного и многократного использования Дезинфекция изделий медицинского назначения проводится с целью уничтожения патогенных и условно-патогенных микроорганизмов - вирусов (в т...

Машины и механизмы для нарезки овощей В зависимости от назначения овощерезательные машины подразделяются на две группы: машины для нарезки сырых и вареных овощей...

Классификация и основные элементы конструкций теплового оборудования Многообразие способов тепловой обработки продуктов предопределяет широкую номенклатуру тепловых аппаратов...

Studopedia.info - Студопедия - 2014-2023 год . (0.002 сек.) русская версия | украинская версия