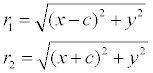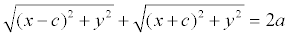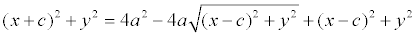Эксцентриситет фигуры эллипс
Определение. Форма эллипса определяется характеристикой, которая является отношением фокусного расстояния к большей оси и называется эксцентриситетом. е = с/ a. Т.к. с < a, то е < 1.
Определение. Величина k = b / a называется коэффициентом сжатия, а величина 1 – k = (a – b)/ a называется сжатием. Коэффициент сжатия и эксцентриситет связаны соотношением: k2 = 1 – e 2. Если a = b (c = 0, e = 0, фокусы сливаются), то эллипс превращается в окружность. Если для точки М(х 1, у 1) выполняется условие: Теорема. Для произвольной точки М(х, у), принадлежащей фигуре эллипс верны соотношения: r 1 = a – ex, r2 = a + ex.
Доказательство. Выше было показано, что r1 + r2 = 2 a. Кроме того, из геометрических соображений можно записать:
После возведения в квадрат и приведения подобных слагаемых:
Аналогично доказывается, что r2 = a + ex. Теорема доказана.
|
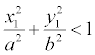, то она находится внутри эллипса, а если 
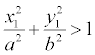, то точка находится вне его.
