Директрисы фигуры эллипс
С фигурой эллипс связаны две прямые, называемые директрисами. Их уравнения: x = a / e; x = - a / e. Теорема. Для того, чтобы точка лежала на границе фигуры эллипс, необходимо и достаточно, чтобы отношение расстояния до фокуса к расстоянию до соответствующей директрисы равнялось эксцентриситету е.
Пример. Составить уравнение прямой, проходящей через левый фокус и нижнюю вершину фигуры эллипс, заданного уравнением:
• Координаты нижней вершины: x = 0; y2 = 16; y = -4. • Координаты левого фокуса: c2 = a 2 – b2 = 25 – 16 = 9; c = 3; F2 (-3; 0). • Уравнение прямой, проходящей через две точки:
Пример. Составить уравнение границы фигуры эллипс, если его фокусы F 1 (0; 0), F2 (1; 1), большая ось равна 2.
Уравнение границы имеет вид: 2 c = по условию 2а = 2, следовательно а = 1, b = Итого искомое уравнение имеет вид:
|
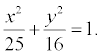
. Расстояние между фокусами:
, таким образом, a2 – b2 = c2 = 1/2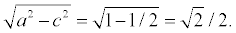
.
