Точки локального экстремума.
Достаточные признаки монотонности функции. Если f ’(x) > 0 в каждой точке интервала (a, b), то функция f (x) возрастает на этом интервале. Если f ’(x) < 0 в каждой точке интервала (a, b), то функция f (x) убывает на этом интервале. Точки локального экстремума. . Число М называется локальным максимумом функции Определение 2. Число m называется локальным минимумом функции Определение 3. Локальный максимум и локальный минимум называются локальными экстремумами. Соответствующая точка Необходимые и достаточные условия существования локального экстремума. Пусть х 0 – точка экстремума (максимума или минимума) функции у = f (x). Тогда в этой точке производная Пусть Пусть Достаточные условия. Если же функция Доказательство. Если Вторая половина утверждения теоремы сводится к первой, если положить Нахождение интервалов монотонности. Найти интервалы монотонности функции f (x) (то есть интервалы возрастания и убывания). Это делается с помощью исследования знака производной f Критические точки. Внутренние точки области определения функции, в которых производная равна нулю или не существует, называются критическимиточками этой функции. Эти точки очень важны при анализе функции и построении её графика, потому что только в этих точках функция может иметь экстремум. Точки, в которых производная функции равна нулю, называются стационарными точками. Наибольшее (наименьшее) значение функции на промежутке называется глобальным экстремумом. Глобальный экстремум может достигаться либо в точках локального экстремума, либо на концах отрезка. График функции y = f(x) называется выпуклым на интервале (a; b), если он расположен ниже любой своей касательной на этом интервале. График функции y = f(x) называется вогнутым на интервале (a; b), если он расположен выше любой своей касательной на этом интервале. Достаточный признак выпуклости функции на интервале. Пусть y = f(x) дифференцируема на (a; b). Если во всех точках интервала (a; b) вторая производная функции y = f(x) отрицательная, т.е. f ''(x) < 0, то график функции на этом интервале выпуклый, если же f ''(x) > 0 – вогнутый.
|

 , если существует такая окрестность точки
, если существует такая окрестность точки 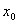 , что для всех
, что для всех 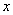 из нее выполняется неравенство
из нее выполняется неравенство 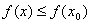 . При этом М=
. При этом М=  , а сама точка
, а сама точка 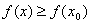 . При этом m=
. При этом m=  равна нулю или не существует.
равна нулю или не существует.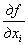 равны нулю (i = 1, 2, …, n), либо хотя бы одна из них не существует.
равны нулю (i = 1, 2, …, n), либо хотя бы одна из них не существует.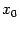 -- критическая точка функции
-- критическая точка функции 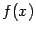 . Если функция
. Если функция  точки
точки 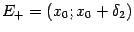 , то точка
, то точка  , то
, то 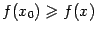 при всех
при всех 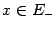 , поскольку из непрерывности
, поскольку из непрерывности  . Точно так же,
. Точно так же, 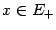 . Выберем из чисел
. Выберем из чисел  и
и  наименьшее:
наименьшее: 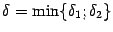 и рассмотрим симметричную окрестность
и рассмотрим симметричную окрестность 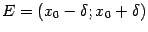 . При
. При 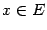 , очевидно,
, очевидно, 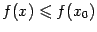 , то есть
, то есть 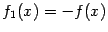 и заметить, что функция
и заметить, что функция  не убывает в
не убывает в  ; локальный максимум функции
; локальный максимум функции 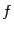 .
. (x). Для этого находят производную f
(x). Для этого находят производную f 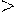 0. На промежутках, где это неравенство выполнено, функция f (x) возрастает. Там, где выполнено обратное неравенство f
0. На промежутках, где это неравенство выполнено, функция f (x) возрастает. Там, где выполнено обратное неравенство f  0, функция f (x) убывает.
0, функция f (x) убывает.


