Точка  называется точкой перегиба графика функции y = f(x), если в данной точке существует касательная к графику функции (она может быть параллельна оси Оу) и существует такая окрестность точки
называется точкой перегиба графика функции y = f(x), если в данной точке существует касательная к графику функции (она может быть параллельна оси Оу) и существует такая окрестность точки  , в пределах которой слева и справа от точки М график функции имеет разные направления выпуклости.
, в пределах которой слева и справа от точки М график функции имеет разные направления выпуклости.
Если функция y = f(x) имеет конечную вторую производную на интервале Х и если выполняется неравенство 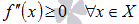 (
( ), то график функции имеет выпуклость направленную вниз (вверх) на Х.
), то график функции имеет выпуклость направленную вниз (вверх) на Х.
Необходимое и достаточные условия перегиба.
Пусть график функции y = f(x) имеет перегиб в точке  и имеет при
и имеет при 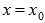 непрерывную вторую производную, тогда выполняется равенство
непрерывную вторую производную, тогда выполняется равенство 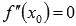 .
.
Пусть функция y = f(x) непрерывна в точке  , имеет в ней касательную (можно вертикальную) и эта функция имеет вторую производную в некоторой окрестности точки
, имеет в ней касательную (можно вертикальную) и эта функция имеет вторую производную в некоторой окрестности точки  . Тогда, если в пределах этой окрестности слева и справа от
. Тогда, если в пределах этой окрестности слева и справа от  , вторая производная имеет разные знаки, то
, вторая производная имеет разные знаки, то  является точкой перегиба графика функции.
является точкой перегиба графика функции.
Если 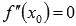 , а
, а 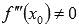 , тогда
, тогда  является абсциссой точки перегиба графика функции y = f(x).
является абсциссой точки перегиба графика функции y = f(x).
Пусть  , а
, а  , тогда если n – четное число, то
, тогда если n – четное число, то  является абсциссой точки перегиба графика функции y = f(x).
является абсциссой точки перегиба графика функции y = f(x).
Асимптоты графика функции.
Если расстояние от точки M кривой y = f(x) от некоторой прямой y = kx + b стремиться к нулю, когда точка M, двигаясь по кривой, удаляется в бесконечность, то прямая y = kx + b называется асимптотой кривой y = f(x).
Асимптоты могут быть вертикальными, наклонными.
Если 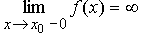 и (или)
и (или)  , то прямая y = x0 является вертикальной асимптотой
, то прямая y = x0 является вертикальной асимптотой
Полное исследование функции:
1. Область определения
2. Точки разрыва и вертикальные асимптоты.
3. Чётность, нечётность, периодичность.
4. Т. Пересечения с осями координат.
5. Исследование по первой производной.интервалы убывания или возрастания,т. Экстремума.
6. Исследование по второй производной, выпуклости вогнутости,точки перегиба.
7. Наклонные и горизонтальные асимптоты.

 называется точкой перегиба графика функции y = f(x), если в данной точке существует касательная к графику функции (она может быть параллельна оси Оу) и существует такая окрестность точки
называется точкой перегиба графика функции y = f(x), если в данной точке существует касательная к графику функции (она может быть параллельна оси Оу) и существует такая окрестность точки  , в пределах которой слева и справа от точки М график функции имеет разные направления выпуклости.
, в пределах которой слева и справа от точки М график функции имеет разные направления выпуклости.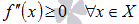 (
( ), то график функции имеет выпуклость направленную вниз (вверх) на Х.
), то график функции имеет выпуклость направленную вниз (вверх) на Х.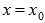 непрерывную вторую производную, тогда выполняется равенство
непрерывную вторую производную, тогда выполняется равенство 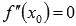 .
.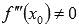 , тогда
, тогда  , а
, а  , тогда если n – четное число, то
, тогда если n – четное число, то 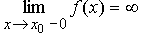 и (или)
и (или)  , то прямая y = x0 является вертикальной асимптотой
, то прямая y = x0 является вертикальной асимптотой


