Показатели сходства, основанные на мерах разнообразия

Выделено 6 мер измерения бета-разнообразия на основе дан­ных по присутствию или отсутствию видов.

Мера Уиттекера описывается формулой:

,

где S – общее число видов, зарегистрированных в системе: a – среднее разнообразие выборок стандартного размера, измеряемое как видовое богатство.

Мера Коуди разработана для исследования изменений в сообществе птиц вдоль средового градиента:

,

где g(H) – число видов, прибавившихся вдоль градиента местообитаний, а l(H) – число видов, утраченное на том же трансекте.

Меры Ратледжа. Мера b_R учитывает общее видовое богатство и степень совпадения видов:

,

где S – общее число видов во всех выборках, а r – число пар видов с перекрывающимся распределением.

Мера b_I основана на теории информации и была упрощена для качественных данных и равного размера выборок:

,

где e_i – число выборок вдоль трансекта, в котором представлен i -й вид, a_j – видовое богатство j - й выборки, а T = å e_i = å a_j.

Мера b_E – экспоненциальная форма b_I:

b_E = exp (b_I) – 1.

Мера Уилсона и Шмидыb_T включает те же элементы утраты (l) и добавления (g) видов, что и мера Коуди, но стандартизована на среднее видовое богатство выборок a, входящее в меру Уиттекера:

b_T = [g (H) + l(H)]/2a.

 

Все 6 критериев были оценены Мэгарран [1992] по 4-м критериям с целью определить лучший показатель:

1) число смен сообществ (выбраны 2 гипотетических градиента, один из которых однороден, т. е. вдоль всей его длины присутствуют одни и те же виды, а другой состоит из неперекрывающихся сообществ);

2) аддитивность (способность индекса давать ту же самую величину бета-разнообразия, независимо от того, высчитывается ли она по данным для двух концов градиента или по сумме значений бета-разнообразия, полученных внутри градиента. Например, при трех точках сбора (a, b, c):

b (a, c) =b (a, b)+ b(b, c);

3) независимость от степени разнообразия сообществ (бедное и богатое видами сообщество);

4) независимость от чрезмерного размера выборки.

Большинству критериев удовлетворяет мераУиттекера b_W.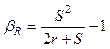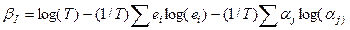