Указать номер рисунка, на котором отрезок AS является диагональю параллелограмма.
Сегодня с помощью специалистов УО «Республиканский институт контроля знаний» попробуем извлечь уроки из тех результатов, которые были получены по итогам проведения ЦТ по математике за последние несколько лет. Полагаем, что это может быть очень полезно будущим абитуриентам и их учителям математики.
Математика по праву считается одним из наиболее сложных школьных предметов. И алгебра, и геометрия – это науки, обучение которым построено по четкому алгоритму: от простого к сложному, при этом каждая последующая тема является прямым или косвенным продолжением предыдущей. С каждым занятием задачи по математике становятся всё сложнее, и, не усвоив материал вчерашнего урока, завтра ученик уже не сможет с ними справиться. Пробелы в знаниях – основная причина восприятия тестов централизованного тестирования как «запредельно сложных», когда решение простейших уравнений кажется непреодолимой задачей, а страх растет перед каждым последующим заданием по сравнению с предыдущим в геометрической прогрессии. Однако заметим, чувство страха не возникает, если прочно усвоен материал за курс средней школы. Все задания, предлагаемые участникам централизованного тестирования по математике, разрабатываются в строгом соответствии с требованиями школьной программы, а также программы вступительных испытаний, учитывающей особенности выпусков двух последних лет, т.е. «запредельно сложных заданий» в тестах нет и быть не может. Кроме того, тесты по математике, как и по любому другому предмету, содержат задания пяти уровней сложности, а это значит, что каждый, даже «случайно зашедший», рассчитывающий «удачно погадать» участник тестирования, может отыскать посильное ему задание и решить его, применив багаж накопленных в школе знаний. Подчеркнем, решить,а не угадать. Интуиция в прошлом году подвела 254 участника тестирования, которым не удалось угадать ни одного правильного ответа. В то же время, выпускники, подзабывшие такие темы школьного курса математики, как линейные и квадратные неравенства, тригонометрические и иррациональные уравнения, попробовали свои силы и правильно решили задания, посредством которых проверялось знание определений геометрических фигур и их элементов, умения определять координаты точек, работать с графиком. Так, например, подавляющее большинство участников тестирования успешно справились с заданием, в котором требовалось: Указать номер рисунка, на котором отрезок AS является диагональю параллелограмма.
Многие правильно определили температуру воздуха в 10 часов по графику, отображающему изменения температуры воздуха от полуночи до полудня.
В задании Точки 1) 5; 2) 3; 3) 4; 4) 3; 5) 4 правильный ответ (
Отметим, что решение приведенных заданий не приносит желаемого количества баллов, так как чем легче задание, тем меньше оно «стоит». Абитуриент, выбравший по собственной инициативе математику в качестве вступительного испытания, должен владеть рациональными вычислительными приемами, знать много полезных формул и уметь их применять в ходе решения уравнений, примеров, задач как части А (18 заданий с выбором ответа), так и части В (12 заданий со свободно конструируемым ответом). В то время как задания части А просты и понятны всем без исключения участникам тестирования, владеющим материалом в рамках школьной программы, задания части В являются самыми сложными, поскольку исключают возможность угадывания и проверяют умения анализировать, синтезировать, обобщать, применять знания в нестандартной ситуации. Большинство заданий части В построены на материале темы «Уравнения и неравенства», позволяющие подготовленным участникам тестирования продемонстрировать умения решать системы линейных неравенств, квадратные неравенства, неравенства с модулем, логарифмические неравенства, системы рациональных уравнений, выбирать наиболее рациональный способ решения показательных, тригонометрических, иррациональных, комбинированных уравнений, а также текстовых задач. Чаще всего ошибки в заданиях данного раздела, связаны с отсутствием четкого представления о понятиях системы и совокупности, о геометрическом смысле модуля, о ходе решения квадратных уравнений, о свойствах числовых неравенств. Во избежание ошибок на предстоящем тестировании, рассмотрим основные идеи решения заданий, вызвавших затруднения у большинства абитуриентов 2009 г.
|

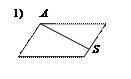
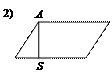
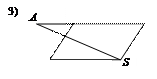



 и
и  расположены на одной прямой, параллельной оси
расположены на одной прямой, параллельной оси 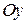 . Значение
. Значение 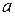 равно:
равно: 4) указали в своих бланках ответов больше половины участников тестирования.
4) указали в своих бланках ответов больше половины участников тестирования.


