Подготовка к работе
Работа № 9 ИССЛЕДОВАНИЕ ИНДУКТИВНО СВЯЗАННЫХ ЦЕПЕЙ
Цель работы: экспериментальное определение параметров двух индуктивно связанных катушек и проверка основных соотношений индуктивно связанных цепей при различных соединениях катушек.
Подготовка к работе Схема замещения двух индуктивно связанных катушек, удовлетворительно учитывающая электромагнитные процессы в диапазоне низких и средних частот, представлена на рис. 9.1, где L 1, R 1 и L 2, R 2 – индуктивности и сопротивления соответственно первой и второй катушек; M – их взаимная индуктивность. Степень магнитной связи двух катушек определяется коэффициентом связи:
где X 1 = w L 1, X 2 = w L 2 – индуктивные сопротивления катушек; XM = w M – сопротивление взаимной индуктивности, при этом 0 £
 
В режиме гармонических колебаний уравнения цепи на рис. 9.1 имеют вид:
Знак M и XM определяется выбором положительных направлений токов I 1 и I 2. Для выбранных направлений токов M > 0, если включение катушек согласное, и M < 0, если включение встречное. Способ включения катушек устанавливается с помощью однополярных выводов, отмеченных «звездочками»: если токи катушек направлены одинаково относительно однополярных выводов (например, как показано на рис. 9.1), то катушки включены согласно; в противном случае включение встречное. Параметры уравнения (9.2) могут быть определены из двух опытов холостого хода, в одном из которых I 2 = 0, в другом I 1 = 0; осуществляют эти опыты размыканием соответствующей пары внешних выводов катушек. Если используют катушки достаточно высокой добротности (w L >> R), то при определении их индуктивности допустимо пренебречь активными сопротивлениями обмоток катушек, т. е. считать R 1 = 0 и R 2 = 0; ошибка при этом будет несущественной с точки зрения инженерной практики. Полагая в уравнениях (9.2) сначала I 2 = 0, а затем I 1 = 0, при условии R 1 = R 2 = 0 получаем соответственно:
На рис. 9.2, а показано последовательное соединение двух индуктивно связанных катушек. В этом случае
Рис. 9.2 Для параллельного соединения (рис. 9.2, б)
В выражениях (9.4), (9.5) M > 0 при согласном и M < 0 при встречном включении катушек. Если к выводам второй катушки присоединить нагрузочное сопротивление Zн, получим двух обмоточный трансформатор (рис. 9.3). В трансформаторе энергия от источника, включенного в цепь первичной обмотки, передается нагрузке Z н, подключенной к вторичной обмотке. Эта передача осуществляется без электрической связи между обмотками посредством изменяющегося потока взаимной индукции. Рассматривая трансформатор как четырехполюсник, можно его передающие свойства характеризовать функциями передачи напряжений и токов. Положив

В случае активной нагрузки (Z н = R н) модуль функции передачи по напряжению (АЧХ)
|

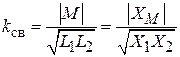 , (9.1)
, (9.1)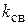 £ 1.
£ 1.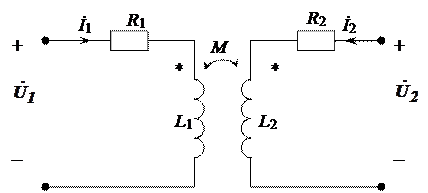
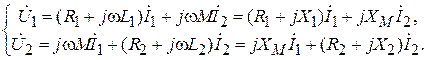 (9.2)
(9.2)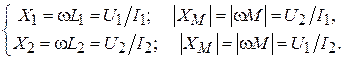 (9.3)
(9.3)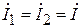 ,
, 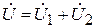 и из уравнения (9.2) при R 1 = R 2 = 0 находим выражение эквивалентной индуктивности:
и из уравнения (9.2) при R 1 = R 2 = 0 находим выражение эквивалентной индуктивности: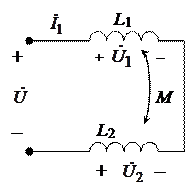
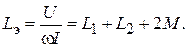 (9.4)
(9.4)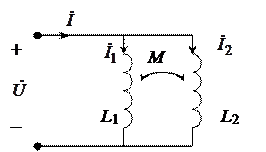

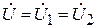 ,
,  . Разрешая систему уравнений (9.2) относительно токов с учетом R 1 = R 2 = 0, можно получить выражение эквивалентной индуктивности:
. Разрешая систему уравнений (9.2) относительно токов с учетом R 1 = R 2 = 0, можно получить выражение эквивалентной индуктивности: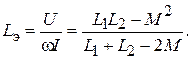 (9.5)
(9.5) , из уравнений (9.2) при R 1 = R 2 = 0 получаем:
, из уравнений (9.2) при R 1 = R 2 = 0 получаем: (9.6)
(9.6)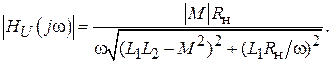 (9.7)
(9.7)


