Зависимость характера переходного процесса от корней характеристического уравнения.
1) Когда характеристическое уравнение имеет один корень, свободный ток определяется формулой iсв = Аеpt = Ае-αt, где р = -α; и зависит только от параметров цепи, А зависит от параметров цепи ЭДС и момента включения. За интервал времени t = τ= Величину τ= 2) Когда характеристическое уравнение имеет два действительных корня неравных корня P1≠ Р2, свободная составляющая определяется как: iсв = А1еp1t +А2е p2t, то есть равна сумме двух экспонент. 3) При P1= Р2 = - α; решением задачи является функция вида: iсв = (А1+А2 t)еpt = (А1+А2 t)е-αt 4) В случае комплексно-сопряженных корней свободная составляющая будет иметь вид синусоидальных затухающих свободных колебаний. Обозначим действительную часть корней буквой δ, а мнимую - ωсв. P1,2= - δ
Свободная составляющая тока описывается формулой: iсв = Ае-δtsin(ω0t+
|
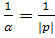, iсв уменьшается в е = 2,71 раза.
. В нашем примере δ= 
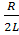- эта величина называется коэффициентом затухания.
- циклическая частота свободных колебаний.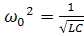
– резонансная частота контура.
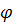), где 
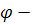начальная фаза, которая определяется вместе с постоянной интегрирования А, и зависит от параметров схемы, начальных условий и величин источников.
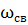и δ зависят только от параметров цепи после коммутации.
