Свойства корней характеристического уравнения.
Число корней характеристического уравнения равно степени этого уравнения. Уравнение первой степени имеет всегда отрицательный действительный (не мнимый и не комплексный) корень. Уравнение второй степени может иметь: б) Два действительных равных отрицательных корня. в) два комплексно-сопряженных корня с отрицательной действительной частью. Возьмем характеристическое уравнение:
Это квадратное уравнение типа ах2+bx+c=0 D= b2+4ac= P1,2= При При При δ ωсв P1,2= - Уравнение третьей степени может иметь: а) три действительных неравных отрицательных корня; б) три действительных отрицательных корня, из которых два корня равны друг другу; в) три действительных равных отрицательных корня; г) один действительный отрицательный корень и два комплексно-сопряженных с отрицательной действительной частью.
|
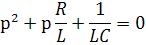
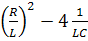
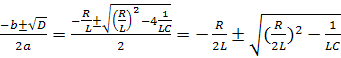
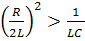мы получаем два действительных отрицательных корня P1 и Р2.
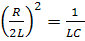, D=0 и оба корня равных P1= Р2 = 
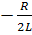; (Rкр)=2 
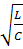этот случай называется критическим.
, дискриминант отрицательный и корень из отрицательного числа дает мнимую составляющую.
