Определение постоянных интегрирования.
Пусть iсв = А1еp1t +А2е p2t + … С помощью уравнений Кирхгофа и законов коммутации нужно найти числовое значение искомого свободного тока при t=0, которое обозначается iсв(+0), а так же числовое значение первой, а если понадобится, то и высших производных от свободного тока, взятых при t =+0, то есть I’св(+0), I’’св(+0) и т.д. Если характеристическое уравнение имеет один корень, то iсв(+0) = Аеp(+0) = А, то есть постоянная интегрирования определяется по величине свободного тока при t=+0. Если корня два и => iсв = А1еp1t +А2е p2t, то iсв = А1+А2 . Однако этого уравнения не достаточно для нахождения обеих постоянных интегрирования => нужно взять производную от iсв(+0) по t.
По второму закону Кирхгофа имеем: i(+0)R+ Uс(+0)+L так как i(+0)=0, то
А1= - А2 i(t) = При нулевых начальных условиях При ненулевых начальных условиях емкость можно считать источником ЭДС с величиной равной При условии, что
При
Когда корни комплексно-сопряженные
|
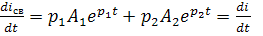, так как iпр = 0;
;
iсв(+0) = 0 = А1+А2 => А1=- А2
= E
, тогда
; 
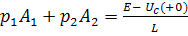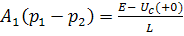
, тогда
*
0, емкость можно считать, а индуктивность iL(+0) = 0 можно считать обрывом ветви.
0, а индуктивность можно считать источником тока величиной равной iL(+0) 
0.
, и оба действительные p1,2 = 
, формула * выглядит так: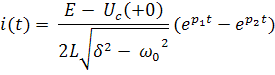
, когда Rкр = 2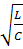 
или 
получаем неопределенность типа 
. Это предельный случай апериодического разряда. Rкр – критическое сопротивление. Эту неопределенность раскрывают по Лапиталю.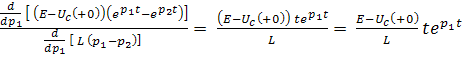
=>
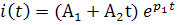
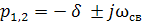, получим: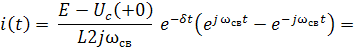
; 
=> 
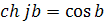
