Способы отображения вариационного ряда

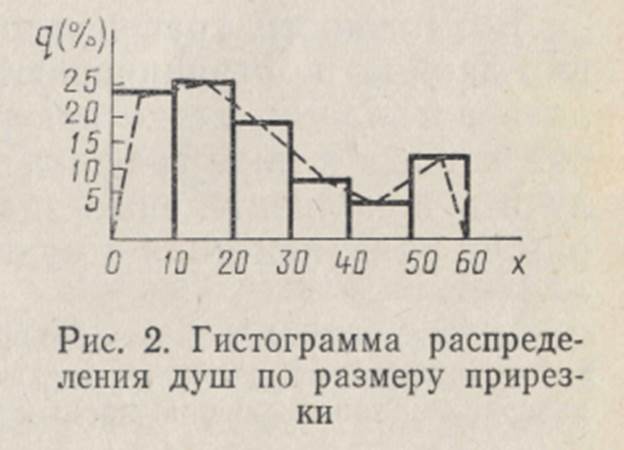
Существует несколько способов графического изображения рядов – полигон, гистограмма и кумулята.

Полигон распределения в основном используется для изображения дискретного ряда, но можно построить полигон и для интервального ряда, если предварительно привести его к дискретному. Полигон распределения представляет собой замкнутую ломаную линию в прямоугольной системе координат с координатами (x_i;q_i), где x_i – значение i-го признака, q_i – его частота или частость. При этом x_i откладывают по горизонтальной оси, q_i – по вертикальной.

Гистограмма распределения применяется для изображения интервального ряда. Для построения гистограммы на горизонтальной оси откладываются последовательно отрезки, равные интервалам признака, и на этих отрезках, как на основаниях, строят прямоугольники, высоты которых рав­ны частотам или частостям для ряда с равными интерва­лами, плотностям — для ряда с неравными интервалами.

Пример 14. Построим гистограмму распределения душ по размеру прирезки в Вельском уезде Смоленской губернии по данным табл. 2 (рис. 2) *.

Размер прирезки	Частости	Накопленные частости	Размер прирезки	Частости	Накопленные частости
До 10	24,5	24,5	31—40	9,7	80,2
11—20	26,7	51,2	41—50	5,8	86,0
21—30	19,3	70,5	51—60	14,0	100,0

 

Как уже отмечалось, для интервального ряда также можно построить полигон распределения. Для этого за значения признака при­нимают середины интервалов и для полученного дискретного ряда обычным способом строят полигон. Полигон распределения можно по­лучить и по готовой гистограмме. Достаточно соединить отрезками прямых середины верхних оснований прямоугольников и замкнуть фигуру описанным способом. Результаты такого построения изображе­ны на рис. 2 пунктирной линией.

Кумулята есть графическое изображение вариационно­го ряда, когда на вертикальной оси откладываются накоп­ленные частоты или частости, а на горизонтальной — зна­чения признака. Кумулята служит для графического пред­ставления как дискретных, так и интервальных вариацион­ных рядов.

Пример 15. Построим кумуляту по данным интервального ряда табл. 2. Предварительно рассчитаем накопленные частости.

Обозначим на горизонтальной оси интервалы (рис. 3). Нижней границе первого интервала соответствует частость, равная нулю, а верхней границе — вся частость этого интервала (24,5). Верхней гра­нице второго интервала соответствует накопленная частость первых двух интервалов (51,2) и т. д.

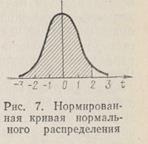
0 10 20 30 40 50 60

Возможности графического изображения статистичес­ких данных не ограничиваются воспроизведением материа­ла в наглядном, легко воспринимаемом виде. Представле­ние данных в виде графика позволяет просто и быстро по­лучить приблизительные значения таких средних характеристик ряда, как мода и медиана. Используя определенные виды графического изображе­ния вариационного ряда, можно приближенно оценить мо­ду и медиану.

2. Закон нормального распределения. Если уменьшать интервалы и одновременно увеличивать число наблюдений в них, то гистограмма распределения будет все более приближаться к плавной линии. Кривая, к которой стремится график при указанном преобразовании, называется кривой распределения.

График нормального распределения представляет собой симметричную одновершинную кривую, напоминающую по форме колокол. Нормальным считается распределение, в котором на признаки вариационного ряда все случайные величины оказывают одинаковое влияние. Форма нормальной кривой и положение ее на оси абсцисс (х) полностью определяется двумя параметрами – средним арифметическим значением и средним квадратичным отклонением s. Ось ординат отражает плотность распределения. При нормальном распределении наиболее часто встречаются величины, близкие к среднему арифметическому, а по мере удаления от среднего значения варианты встречаются все реже.

Каждому значению признака х соответствует при этом определенное значение так называемой функции распреде­ления F(x), показывающее, какова вероятность существо­вания вариант, меньших данного значения х. Геометричес­ки вероятность вариант, меньших х, изображается площадью под кривой слева от точки х. Площадь под всей кривой рав­на 1, что соответствует полной достоверности (т. е. вероят­ности того, что признак примет вообще какое-то значение). Таким образом, видно, что функция распределения F(x) обобщает понятие накопленной частоты вариационного ряда.

Ввиду своей важности для практических приложений функция нормального распределения табулирована, т.е. имеются таблицы, где каждому значению х ставится в со­ответствие вероятность F(x) существования значений, ме­ньших х. Для удобства табулирования в качестве значений признака берутся не сами величины х, а так называемые нормированные отклонения их от среднего значения t, где .

При замене х на t центр распре­деления смещается в точку 0, а еди­ницей измерения становится вели­чина среднего квадратического от­клонения s, но вид кривой распре­деления не изменяется. Среднее зна­чение нормированного отклонения t равно нулю, а его среднее квадратическое отклонение равно единице (рис. 7).

Нормированная функция нормального распределения облада­ет следующими свойствами: F(—¥) =0; F(¥) = l; F(0)=1/2; F(—t) = 1—F(t). То есть, если нормированное распределение признака равно t = 2, то F(t) =0,97725. Соответственно, в 97 случаев из 100 значения признака не отклоняются от своего среднего не более чем на 2s. На рис. 7 площадь, соответствующая этой вероятности, за­штрихована.

Довольно часто приходится определять вероятность того, что нормированное отклонение не превысит по модулю некоторой величины t, т.е. значения признака х отклоняют­ся от своего среднего не более чем на ts. Это вероятность обозначается Ф(t) и равна F (t) — F( — t)=2F(t) —1. Чаще всего на практике используется именно вероятность Ф(t), поэтому эта функция также табулирована. Найдем, например, вероятность того, что нормированное от­клонение по модулю не превышает 2, другими словами, зна­чения признака х отличаются от своего среднего по модулю не более чем на 2s (|t|£2). По табл. 1 приложения вели­чине t = 2 соответствует Ф(t) =0,9545, т.е. примерно в 95 случаях из 100 значения признака отклоняются от своего среднего не более чем на 2s.

При использовании статистических методов часто воз­никает задача проверки нормальности распределения, поскольку нормальность является существенным ус­ловием их корректного применения.

Любой вариационный ряд с нормально распределенными признаками, подчиняется закону нормального распределения. Закон нормального распределения (часто называемый законом Гаусса) играет очень важную роль в теории вероятностей и занимает особое место среди других законов. Суть его сводится к следующему. Зная среднее арифметическое значение среднее квадратичное отклонение s мы можем спрогнозировать математическое ожидание плотности распределения значений изучаемого явления. Математическое ожидание . 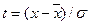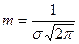При этом при построении графика на оси абсцисс откладывается математическое ожидание. При нормальном распределении математическое ожидание m равно медиане вариационного ряда и равно приведенной средней арифметической . В том случае, если эти показатели совпадают, мы можем говорить о нормальном распределении, и наш вариационный ряд является нормально распределенным и подчиняется закону нормального распределения. Используя математические вычисления, можно доказать, что если случайная величина распределена нормально, то абсолютная величина ее отклонения от математического ожидания не превосходит утроенного среднего квадратического отклонения. Это так называемое правило трех сигм. На практике это означает, что если распределение случайной величины не известно, но условие, приведенное в данном правиле, выполняется, то есть основание предполагать, что изучаемая величина распределена нормально.